

Volume 9, No. 3, Art. 32 – September 2008
Video Analysis of Mathematical Practice? Different Attempts to "Open Up" Mathematics for Sociological Investigation
Christian Greiffenhagen
Abstract: In this article I argue that in contrast to a large number of sociological studies of laboratory practices in the natural sciences, there have been relatively few studies that have investigated professional mathematical practice. I discuss three different methodological attempts to "open up" advanced mathematics for sociological investigation: (1) LIVINGSTON's "demonstrative sociology"; (2) MERZ and KNORR-CETINA's "e-mail ethnography"; and (3) my own "video ethnography."
Key words: video analysis; workplace studies; sociology of scientific knowledge; mathematics
Table of Contents
1. Introduction: The Rise of the Sociology of Scientific Knowledge
2. What About Mathematics?
2.1 LIVINGSTON's "demonstrative sociology"
2.2 MERZ and KNORR-CETINA's "e-mail ethnography"
2.3 My "video ethnography"
2.3.1 Case study of mathematical lectures
2.3.2 An exemplar
2.3.3 What does this fragment tell us about (professional) mathematics?
3. Conclusion: Video Analysis of Mathematical Practice?
1. Introduction: The Rise of the Sociology of Scientific Knowledge
For a long time, scientific and mathematical knowledge were seen as beyond the remit of the social sciences. Of course it would be possible to determine the social factors that are at play among scientists, who, after all, form a social group just like other (e.g., political or religious) organizations, but what could be social about the content of science, i.e. scientific laws (e.g., Newton's Laws of Motion) or mathematical theorems (e.g., Pythagoras Theorem)? Both seem to be eternal and universal statements which do not vary with the passage of time and changes in social conditions. [1]
Thus in most readings of MANNHEIM's (1936) sociology of knowledge—which aimed to exhibit, in a generalization of Marx's theory of ideology, how forms of thought (e.g., religious or political beliefs) were determined by social interests—the natural sciences and mathematics were seen to be excluded from the remit of the sociology of knowledge. Since knowledge in the natural sciences seems to follow from "the nature of things" and knowledge in mathematics from "pure logical possibilities" (MANNHEIM, 1936, p.239; quoted in BLOOR, 1976, p.8), they seem to be free of any social factors. As a consequence, the sociology of science was seen to be restricted to a "sociology of scientists" (LATOUR, 2005, p.95), that is, the study of the social structure of the community of scientists, or a "sociology of error" (BLOOR, 1976, p.8), that is, the study of the ideological or political influences that led scientists away from the truth.1) [2]
The most influential book in changing the sociology of science was Thomas KUHN's (1962/1996) The Structure of Scientific Revolutions, in which KUHN challenged the traditional image of (natural) science as being continuously cumulative or straightforwardly progressive.2) This image, KUHN claimed, was based on a distorted reading of the history of science, which acknowledged past achievements only in relation to present concerns (i.e., earlier scientific theories were valued only according to the way they contributed to current scientific theories). Rather than seeing the progress of science as a succession of theories that ever closer approach reality (where each new theory is a continuous improvement on previous ones), KUHN argued that successive theories are significantly discontinuous with each other. KUHN used the expression "incommensurable" to capture the fact that two theories cannot be compared in a wholesale way, i.e., that it is impossible to ascertain one of the two as being better in all respects. In particular, KUHN pointed out that what counts as evidence is itself in disagreement amongst the theories. KUHN suggested that the idea of "scientific revolution" be taken rather literally, i.e., that change from one scientific theory to another is brought about through the overthrow of one group (subscribing to the old theory) by another (associated with the new one). Contest between groups decides which theory is accepted within the scientific community and therefore determines what will "count" as scientific knowledge. [3]
KUHN's picture of science led to the view that neither "logic" nor "evidence" is sufficient to decide which scientific theory is correct, but that social factors play an important role. This gave rise to the "new" sociology of scientific knowledge (cf., LYNCH, 1993, Chapter 3), most famously expressed in BLOOR's (1976, p.1) "strong programme":
"Can the sociology of knowledge investigate and explain the very content and nature of scientific knowledge? Many sociologists believe that it cannot. They say that knowledge as such, as distinct from the circumstances surrounding its production, is beyond their grasp. They voluntarily limit the scope of their own enquiries. I shall argue that this is a betrayal of their disciplinary standpoint. All knowledge, whether it be in the empirical sciences or even in mathematics, should be treated, through and through, as material for investigation." [4]
BLOOR's explicit aim was to open up the very content of scientific and mathematical knowledge for sociological investigation, and his largely programmatic writings have stimulated a multitude of empirical case studies, predominantly of the natural sciences. Most of these studies employed one of the two following research strategies to demonstrate the social character of scientific knowledge: [5]
(1) Some studies used historical materials of scientific controversies and investigated how these controversies were resolved. These studies, among which is SHAPIN and SHAFFER's (1985) famous study of the dispute between Robert Boyle and Thomas Hobbes, argued against the view that a scientific theory was successful simply because it was "true." To the contrary, they argued that throughout history scientific arguments were often not settled by any "decisive" experiment that proved one theory wrong and another right, but rather involved in a certain sense "external" elements, like rhetoric or the recruitment of allies. Thus COLLINS and PINCH (1993, Chapter 4) discuss the debate between Louis Pasteur and Felix Pouchet in order to show that although Pasteur "won" this debate, this was not as a result of "the neutral application of scientific method" (p.85), but by holding on to his theory despite seemingly contrary experimental evidence. [6]
(2) While the first type of study originated in history, the second type of study was inspired by anthropology and sociology. A variety of researchers conducted observational studies of the day-to-day work practices of laboratory scientists. These studies are often referred to as "laboratory studies" (e.g., LATOUR & WOOLGAR, 1979; KNORR-CETINA, 1981; LYNCH, 1985) and frequently contrasted idealized portrayals of science (as, e.g., operating through the hypothetico-deductive method) with how science actually gets done in the laboratory. In particular, these studies showed that a published scientific article, which presents scientific work as a planned, logical activity, is only a retrospective account of the actual laboratory work and therefore "hides more than it tells on its tame and civilized surface," since "it deliberately forgets much of what happened in the laboratory" (KNORR-CETINA, 1981, p.94). Scientists, rather than following an idealized scientific method, work in a practical, situated, and occasioned manner, i.e., as "tinkerers" (p.34). [7]
Both types of empirical case study of scientific knowledge have presented a challenge to more traditional pictures of science. However, almost all the studies have focused on the experimental sciences. That is to say, while BLOOR explicitly wanted a sociology of empirical science and mathematics, the latter was by and large neglected:
"Although mathematics was central to David Bloor's early discussion of the 'strong programme of the sociology of knowledge', most subsequent strong-programme work has been on the natural sciences. The deductive proofs at the centre of mathematics and logic have seldom been addressed in any detail." (MACKENZIE, 1999, p.7) [8]
BLOOR's own work on mathematics was particularly concerned with demonstrating the conventional nature of mathematics, e.g., "the conventional components of the concepts '2' and '4' and 'addition'" (BLOOR, 1994, p.21). BLOOR argued that most people think that "2 + 2 = 4" expresses an empirical fact (i.e., a statement about reality) or a logical fact (i.e., a fundamental logical principle). BLOOR pointed out that 2 + 2 only equals 4 in our decimal system and that other arithmetic systems (e.g., a tertiary system in which 2 + 2 equals 113)) are equally "natural" or "logical." Since it is a purely contingent matter that we have adopted the decimal system, "2 + 2 = 4" can be said to be a social fact.4) [9]
There have been few attempts to follow through BLOOR's claim that it should be possible to study mathematics sociologically. The few studies that do exist are almost all of the first type discussed above, i.e., historical case studies of how controversies and debates in mathematics are resolved and under which conditions statements are "accepted" into the mathematical corpus. The most famous of these is Imre LAKATOS's (1976) Proofs and refutations, a study of the historical development of Euler's conjecture, which illustrates that definitions of concepts used in mathematics (such as "edge" or "polyhedra") are not fixed but are flexible and can "grow." Similarly, MACKENZIE (1999, 2001) studied the use of computers in modern mathematical proofs (e.g., as part of the famous Appel-Haken solution to the Four-Color Conjecture), in order to demonstrate that not just mathematical concepts, but the very notion of mathematical proof (what counts as a mathematical proof) is not fixed. PICKERING (1995, Chapter 4) investigated Hamilton's construction of quaternions to exhibit that in the process of creating new mathematical knowledge, while there are no pre-established paths to follow, the new creations have nevertheless to fit in with pre-existing disciplinary conventions. [10]
There is almost a complete absence of anthropological or sociological studies of professional mathematics. In other words, there have been no "laboratory studies" of mathematical practice. One possible reason for this is that in contrast to the experimental sciences, where scientists work together in a designated place using a variety of instruments, mathematicians typically work alone (very often in their office or home—but also on buses and trains), using only pen and paper to do their work. A solitary (silent) mathematician scribbling on a piece of paper might make a less immediate sociological object than a buzzing scientific laboratory where scientists talk to each other and use a number of instruments. The most visible aspects of mathematical work are the symbols that appear on boards or pieces of paper, but it would be difficult to see the sense of these symbols without a few years of training. Observational studies of mathematical practice therefore are inherently difficult. [11]
The few attempts of conducting an empirical investigation of mathematical practice have thus all come up with different methodological solutions for the practical and technical problems in doing so. In the following, I discuss three approaches: LIVINGSTON's "demonstrative sociology" of mathematical proofs, MERZ and KNORR-CETINA's "e-mail ethnography" (my term) of theoretical physics, and my own "video ethnography" of graduate lectures in mathematical logic. [12]
2.1 LIVINGSTON's "demonstrative sociology"
LIVINGSTON's (1986; 1987, pp.86-141; 1999; 2006) study of mathematics started like a traditional anthropology: LIVINGSTON enrolled in several courses in mathematics and spent several years acquiring the competence necessary to understand what the "natives" were doing. LIVINGSTON learned both the "language" of mathematics, as well as observed mathematicians in lectures, seminars, and workshops. [13]
LIVINGSTON approaches mathematics from the analytic perspective of ethnomethodology (e.g., GARFINKEL, 1967, 2002; LYNCH, 1993), which argues that social scientists tend to produce reports of practices that are subsequently taken as disengaged representations of the practice and thereby miss or neglect the fact that such reports are inextricably tied to the taken-for-granted details of the actual doing of the practice (cf., GARFINKEL, 1967, pp.23-24; GARFINKEL in HILL & CRITTENDEN, 1968, pp.112-113; LYNCH, 1993, p.290). LIVINGSTON therefore does not provide "reports" of what he observed in lectures, seminars, and workshops, but uses his acquired competence to develop what he calls a "demonstrative sociology" (2006, p.64), in which he does not talk "about" mathematics, but invites readers to go through some simple proof for themselves in order to experience the more general points that LIVINGSTON wants to make about proving. LIVINGSTON's "demonstrative sociology" is thus a didactic exercise, in which he provides readers with the necessary knowledge to be able to do a particular mathematical proof. Demonstrating the proof in this way, LIVINGSTON is able to point out some "seen but unnoticed" (GARFINKEL, 1967, p.36) features of mathematical practice. [14]
A brief illustration of the kind of observations that LIVINGSTON makes can be gained from his study of the way that we perform columnar addition (LIVINGSTON, 1995, pp.32-36).

Figure 1: An example of columnar addition5) [15]
This is how LIVINGSTON tries to make visible the work that is involved in performing the first half of the columnar addition:
"We begin at the top of the right column with every intention of working sequentially from top to bottom and, therein, keeping our place in the calculation and doing it 'properly'. Adding 3 and 5, we get 8. But then we see that adding 9 and 1 gives 10 (Figure 3 [in Figure 2 below]). Adding 10 and 8 is easy—we 'replace' the 0 in the 10 with 8 and 'say' (perhaps quite literally) 18, at the same time that we move our pencil so that it is now positioned on the 7. The 8 in the 18 and the 7 make 15, and 15 and 10 make 25, so we have 25; then we add 5 to get 30. Adding 4 to 30 is easy; having just 'said' 30, we now 'say' 34. This much at least has been straightforward. Now we get busy: 3 is just 3 and it is a lot easier simply to tap 3 out with our pencil, counting as we go, the tapping keeping a mechanical rhythm to allow us to remember that we give just three counts: 35, 36, 37. Figure 4 [in Figure 2 below] has been marked with three dotes to indicate this process.
The sum to this point is 37, and the next number to add is 9. When adding 9 to a number, we know that the one's digit in that number goes down one—so the 7 in 37 goes to 6—and the digit in the ten's place goes up one, from 3 to 4. So we have 6 and a carry of 4, which we write at the top of the column on the left (Figure 5 [in Figure 2 below])." (pp.33-34)
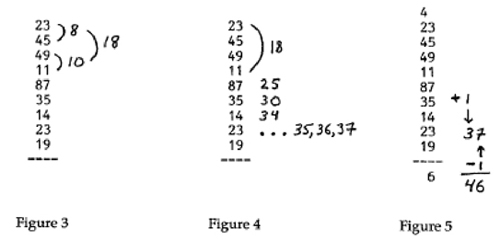
Figure 2: Doing the columnar addition6) [16]
LIVINGSTON aims to draw attention to the "seen but unnoticed" features of activities, either those that are relatively familiar to most readers (such as columnar addition) or those that are more esoteric to many readers (such as mathematical theorem proving). In the case of mathematics, LIVINGSTON points to:
the practical nature of proving (even though mathematicians are working according to logical laws, mathematicians do not operate "automatically" as if those laws worked like a computer program and prescribed each next step; mathematicians have to work out what the next step could/should be and how each steps follows from the next);
the social nature of proving (even when mathematicians are working alone in their room, the moves that they make are part of a shared, standardized, disciplinary practice); and
the retrospective-prospective nature of proving (although proofs have a linear structure, understanding how a proof works proceeds both prospectively, i.e., involves anticipating where a particular step might lead to, and retrospectively, i.e., entails seeing the reason for doing a previous step). [17]
The biggest advantage of LIVINGSTON's way of approaching mathematics is that it gives direct access to an esoteric practice. As a reader of one of LIVINGSTON's papers (or as a member of the audience at one of his presentations), one does not just read about mathematics, but is rather instructed in actually doing it. By choosing his examples from basic arithmetic or geometry, LIVINGSTON is able to dispel misconceptions about mathematics, in particular, the belief that mathematics is a simple application of logic and therefore a form of "cold" deductive reasoning, where each next step is dictated by its predecessor. LIVINGSTON's demonstrations reveal that a lot of practical, situated work is involved in figuring out how to move from one step to the next. [18]
Since LIVINGSTON needs to give the reader all the necessary knowledge to understand a particular proof, his strategy is however limited to relatively simple examples (predominantly high school level geometry problems). In only one place does LIVINGSTON try to extend his strategy to a more complex proof, that of Gödel's Incompleteness Theorem (LIVINGSTON, 1986). However, in contrast to his demonstrations of more simple proofs, LIVINGSTON's exposition of this more advanced proof remains inaccessible to a technically untrained readership and seems to point to a limitation of his "demonstrative sociology." Mathematical knowledge and competence has a strongly hierarchical organization, so Gödel's proof is dependent on various other branches of mathematics (e.g., number theory, analysis, formal logic) and it is therefore difficult to instruct the reader in how the proof works without giving an introduction to all those different branches of mathematics. [19]
This limitation in LIVINGSTON's strategy points to another question: LIVINGSTON exhibits the details of the work of proving, but is less specific on the purposes for which, or the situations in which, this proving is done. There are differences between an undergraduate studying a proof for the first time, a lecturer re-familiarizing her- or himself with a particular proof before a lecture, or a research mathematician browsing through some recently published proofs to generate ideas for tackling a problem that the mathematician is currently working on. Just as there is a plurality of ways of, and a purpose for, reading ordinary texts (SHARROCK & IKEYA, 2000, p.274), so there is a plurality of ways of, and purposes for, reading mathematical proofs. LIVINGSTON's strategy, which in a certain sense abstracts from any concrete situation or purpose of reading a proof, is therefore strangely acontextual. LIVINGSTON is keen to render mathematical reasoning as a branch of practical activity in order to show that the ways in which mathematicians face problems include those in which anyone does (such as the dependence of sense on context, the consequent dependence of intelligibility upon sequential context, and the retrospective-prospective determination of sense). As a consequence, LIVINGSTON tends to be less concerned with the mathematical relevancies and constraints that enter into even his relatively simple examples. [20]
In sum, LIVINGSTON's "demonstrative sociology" tries to solve the problem of accessing mathematical practice for sociological investigation by developing a "demonstrative sociology" which focuses on providing the reader with the experience of "doing" mathematical work and gives LIVINGSTON the opportunity to point to certain taken-for-granted features of that work. However, he can do so only for relatively simple examples and it is difficult to see how his approach could be extended to investigate more difficult aspects of mathematical practice (e.g., graduate lectures or research mathematicians developing new proofs). [21]
2.2 MERZ and KNORR-CETINA's "e-mail ethnography"7)
While LIVINGSTON chooses "simple" examples (predominantly from high-school level geometry) to approach mathematics, MERZ and KNORR-CETINA (1997) start with an explicitly "difficult" case, namely cutting-edge research in theoretical physics8) at CERN, the European Laboratory for Particle Physics. MERZ and KNORR-CETINA are explicit in their aim of extending the "laboratory study" approach of the experimental sciences to study the "thinking" science of theoretical physics, but are also upfront about the difficulties of doing so:
"When theoretical physicists do a calculation, when they compute the BRST cohomology of the W-algebra, when they grade by
the ghost number or face the
Tb γγ term or when they discuss the advantage of doing H(M⊗M*) over H(F⊗F), students of science usually look the other way. Are these sorts of operations still within the scope of our interest? More
important perhaps, are they even within our reach? Can we study them ethnographically or observationally? What, if one could
study them, might one find out?" (1997, p.73) [22]
MERZ and KNORR-CETINA note that most theoretical physicists work at their desk with pen and paper, an activity which does not lend itself to direct observation. Furthermore, what the physicists are doing is often opaque—even to other physicists working in a different area (let alone to the ethnographer). In contrast to traditional "laboratory studies" of the experimental sciences, MERZ and KNORR-CETINA's study is thus not predominantly based on observations of an ethnographer hanging around in a scientific laboratory, but rather on the e-mail correspondence of physicists (who often cooperate in small groups of 2-4 people), which worked as "prompts" for more detailed discussions with physicists (which benefited from MERZ's training in physics). In other words, MERZ and KNORR-CETINA adapted the anthropological approach to laboratory science for their study of theoretical physics:
"It also has to be admitted that the laboratory approach had to be adapted to the obdurateness of the field: the study is based rather less on the observation of physicists' activities than on one analyst's capability to exploit her physics training and interact with participants as a member of their culture. It is also anchored in a close 'reading' of physicists' personal-professional communications (their e-mail correspondence […]), their calculation protocols, and their explanations to us, which invariably involved paper and pencil. The close 'reading' was adopted to gain access to the ethnomethods implicated in doing theoretical physics work." (MERZ & KNORR-CETINA, 1997, p.74) [23]
MERZ and KNORR-CETINA studied one group of theoretical physicists working on a particular problem. They note that physicists often "get stuck," which happens when physicists lose confidence in the path they pursue and are not sure which alternative to choose, or whether there are any alternatives. As one physicist puts it in an e-mail: "It seems we're stuck. I have no earth-moving new ideas, but instead of keeping silent let me just communicate some loose thoughts in the hope that somebody can do something with them." (p.104) [24]
MERZ and KNORR-CETINA are interested in the different ways in which physicists get "unstuck." They describe that physicists may try to compute the problem by hand, which sometimes allows them to simplify the equations they are working on, but does of course not always work ("computations really get totally out of hand," p.90). Or physicists may try to make a "guess" at a particular solution, which can be tested (a wrong guess will lead to a contradiction); a successful guess may transform a system of 500 equations with 500 unknowns to a system of 500 equations with 50 unknowns. Alternatively, physicists may try to work with specific examples in order to get a "feel" for the problem ("At the moment I don't have a good idea how to make progress, so I'm playing around with examples to see whether I can possibly discover a 'hidden structure'," p.97). [25]
MERZ and KNORR-CETINA's study is noteworthy for trying to study the creation of new knowledge. While both LIVINGSTON and I (see below) investigate the ways in which mathematicians work within an existing body of knowledge, MERZ and KNORR-CETINA study sociologically what theoretical physicists are doing in situations where they do not know how to proceed. MERZ and KNORR-CETINA show that theoretical scientists do not follow an abstract "scientific" or "logical" method, but rather have to work things out in a practical and situated manner (and have different strategies to try to get "unstuck"). [26]
MERZ and KNORR-CETINA's strategy however comes at a price: they cannot give the reader access to the technical details of the work they are studying and instead have to rely on using analogies, metaphors, or similes. For example, they employ the notion of "deconstruction" to characterize the struggles that physicists encounter in their work on mathematical equations, and they make an explicit analogy between writing literary texts and mathematical-physical activity (p.76). The necessity for this strategy is partly a result of the fact that the researchers themselves did not have complete understanding of the technical intricacies involved in the physicists' research:
"The complete collection of e-mails (all in English) exchanged between N, P and A and related to the W-gravity computation was available to us for analysis. However, without N acting as interpreter, the e-mails would have remained Double Dutch for us!" (pp.110-111) [27]
In sum, MERZ and KNORR-CETINA are confronted with typical access difficulties to a highly esoteric and technical practice. Since the work that they are observing is collaborative and conducted in the form of e-mail exchanges between a small group of scientists scattered geographically, they take advantage of the fact that the work of the scientists is to some extent "self-recording." MERZ and KNORR-CETINA do not take the e-mail exchange as their data (in order to analyze it as though it were the phenomena), but rather use it as a conduit for getting the scientists to reflect on, in more vernacular terms, what was going on. The danger of this strategy is that the resulting metaphorical descriptions (e.g., theoretical physics as "deconstruction") might suggest that this practice is, "really," not very different to other practices (e.g., literary criticism). However, the advantage of their approach is that MERZ and KNORR-CETINA, unlike LIVINGSTON, provide a description of people seriously and professionally engaged in doing innovative theoretical physics in a particular situation for a particular purpose. [28]
Both LIVINGSTON and MERZ and KNORR-CETINA have developed their own way to deal with the difficulties of studying theoretical work sociologically. My own work contributes a third approach, distinct from these, but retaining what I believe to be the positive features of them. [29]
As for LIVINGSTON and MERZ and KNORR-CETINA, my own mathematical competence (I studied mathematics for four years) is a crucial prerequisite for this kind of research, trying to follow GARFINKEL's (2002, p.212) recommendation that as a work maxim the analyst should be competent in the practice that he or she is investigating. However, being competent does not tell you how to design a study. While LIVINGSTON moves away from concrete situations of mathematical practice to supply the reader through his "demonstrative sociology" with experiential access to some features of (mostly quite basic) mathematical competence, and while MERZ and KNORR-CETINA exploited the practical features of their field site, namely the collaboration via e-mail exchange of a group of physicists, my own strategy was to find situations in which mathematical competence is accountably visible, i.e., where the accessibility and availability of the practice to an onlooker is an ordinary part of the practice or setting. An explicit aim was to find cases of "advanced" (professional) mathematics, rather than cases of mathematical practice in schools or as part of everyday activities such as grocery shopping or carpentry. Since research mathematics is often pursued alone and in private reflection, these would have to be situations in which two or more mathematicians are coming together to carry out their mathematical reasoning through discussion (often at a board). [30]
Graduate lectures were identified as a first possible site. Although a lecture is predominantly a monologue, it is nevertheless in a certain sense an interactional event, since the lecturer is not talking for himself, but rather for the students. In other words, mathematical lectures are situations in which an experienced mathematician demonstrates mathematical expertise to novices as an important part of their progressive induction into professionally competent autonomous mathematical practice. This setting allows us to see what mathematicians themselves treat as important or noteworthy. [31]
However, looking at mathematical lectures only gives us access to existing mathematical knowledge (and only the demonstration of this knowledge for a particular set of recipients, namely graduate students). The weekly supervision meetings between a supervisor and his doctoral students were therefore chosen as a second site. In these supervision meetings doctoral students present the current state of their research to the supervisor and they collaboratively try to find solutions for problems for which there are as yet no solutions. In these discussions, mathematicians explain to each other their reasons for why a particular way of proceeding might be successful (or not) and thereby have to explicitly formulate some of the strategies, tricks, and competences that they employ when working out novel mathematics. [32]
Both settings were chosen because the people in that setting intend to make mathematical practice visible, and accountably so. That is, the visibility of the mathematical competence is an ordinary part of the practice and therefore amenable to observational study as well as recording. Like LIVINGSTON, my work has been informed by ethnomethodology (GARFINKEL, 1967, 2002; LYNCH, 1993) and conversation analysis (SACKS, 1992; SCHEGLOFF, 2007), which aim to exhibit the endogenous orderliness of activities. By choosing situations in which the participants make aspects of mathematics visible to each other, it is possible to approach mathematics in a naturalistic fashion "from within." Like many analysts working in this tradition, the use of video allows the analyst to capture the situated, accountable practices of the mathematicians, and thereby make these practices amenable to more detailed scrutiny than in more traditional forms of ethnographic observation. As MACBETH (1990, p.191) put it: "As a matter of faithfulness to the texture, temporal shape and material detail of the scenes they record, the video of filmic record provides remarkably uninterpreted renderings of the field." The use of video thus allows us to reveal a "a tacit, but not unknown, social order" (WATSON, 1998, p.208; my emphasis) and has for the last two or three decades been used to study a variety of work practices (e.g., HEATH & LUFF 1992, 2000; HINDMARSH & HEATH, 2000; GOODWIN, 1994, 1995; GOODWIN & GOODWIN, 1996; LYNCH & MACBETH, 1998; KNOBLAUCH, SCHNETTLER, RAAB & SOEFFNER, 2006; MONDADA, 2003, 2007; LINDWALL & LYMER, 2008). [33]
2.3.1 Case study of mathematical lectures
The remainder of the paper will discuss a particular example from the "video ethnography" of graduate lectures in mathematics, before concluding the methodological discussion. [34]
The perhaps most remarkable feature of mathematical lectures is the fact that the lecturer spends most of the time writing at the board. In other words, the lecturer is predominantly not talking "about" mathematics, but actually "doing" mathematics at the board by going through established proofs for the student audience (see also MERZ, 1998). In other words, the lecture can be thought of as a recipient-designed demonstration of mathematical reasoning. One reason for this lies in the fact that the focus of mathematical knowledge is not so much on the results (the theorems), but rather on the ways of establishing these results (the proofs):
"[…] proofs rather than the statement-form of theorems are the bearers of mathematical knowledge. Theorems are in a sense just tags, labels for proofs, summaries of information, headlines of news, editorial devices. The whole arsenal of mathematical methodologies, concepts, strategies and techniques for solving problems, the establishment of interconnections between theories, the systematisation of results—the entire mathematical know-how is embedded in proofs. When mathematicians pick up a paper for study, they turn their attention to the proofs, since proofs are the centre of gravity of a research paper." (RAV, 1999, p.20)
"The ability to construct proofs in advanced mathematical domains is a crucial skill for any mathematician. Indeed, this ability is often the primary goal of advanced mathematics courses and typically the only means of assessing students' performance." (WEBER, 2001, p.101) [35]
Despite some attempts to teach the skill of proving directly (e.g., PÓLYA, 1945), it is generally acknowledged that this skill can only be taught indirectly, namely by observing experienced mathematicians doing proofs (in lectures) and/or by doing simple proofs yourself (in tutorials and exercise classes). The lecture, then, resembles a familiar master-apprentice situation (e.g., in carpentry) where the master goes through a familiar set of moves in an exaggerated way for the benefit of novices, in the hope that some of the novices will be able to pick up on what is important and what is not (and it is important to remember that students are expected to work through weekly 'problem sheets' in order to practice what they have learned in lectures). In short, lectures are attempts to make mathematical reasoning discernible to students. [36]
The lecturer spends most of the time "writing-talking" the proof at the board, where the "writing" and "talking" part are mutually elaborative (in fact, very often the lecturer is writing almost exactly what he is saying, or, vice versa, saying almost exactly what he is writing). However, there are occasional episodes when the lecturer interrupts the written exposition of the proof on the board, in order to make some additional remarks to the class. Such episodes are often marked in some way (e.g., the lecturer typically stands away from the board and faces the student audience) and frequently consist of various "glossing practices" or "formulations" (cf., GARFINKEL & SACKS, 1970; HERITAGE & WATSON, 1979, 1980). These typically occur at the beginning of a proof (projecting what will be done), at the end of a proof (summarizing what has been done), or, in long proofs, after a particular part has been completed (summarizing what has been done so far and projecting how this will be used in subsequent parts). [37]
An example of this occurs is the following fragment, taken from the fifth lecture of a course in inductive logic. The lecturer wants to prove the following theorem:

Theorem 1.9. Suppose w (⋅ | ⋅) is a fair conditional belief function. Then w is a conditional probabilistic belief function.9)
Figure 3: The theorem to be proved [38]
The proof for this theorem is relatively long (lasting almost forty minutes). The lecturer starts the proof by unpacking the definitions in the theorem formulating what it is that they need to show. It turns out that in order to prove that w is a conditional probabilistic belief function, it is enough to show that the following equation holds10):

w (θ | φ) · wη (φ) = wη (θ ∧ φ)
(read: "doubleyou theta given phi times doubleyou eta phi
is equal to doubleyou eta theta and phi")
Figure 4: What needs to be shown [39]
Schematically, the aim is to prove that A · B = C11). Rather than doing so directly, this is shown indirectly, by considering two cases that are revealed not to be possible (this strategy is often called a "proof by contradiction"). As a first case, it is assumed that A · B < C, and it is shown that this assumption leads to a contradiction. As a second case, it is assumed that A · B > C, which also leads to a contradiction. Since it is neither possible that A · B < C nor that A · B > C, it can be concluded that A · B = C (this kind of argument makes use of the law of the excluded middle). [40]
Having outlined the general proof strategy, the lecturer starts to work through the details of the first case, i.e., assumes that A · B < C with the aim of showing that this assumption will eventually lead to a contradiction (Figure 5).

Figure 5: Case 1 [41]
In two preliminary steps, the lecturer first shows that B < 112) and subsequently that also A < 113) (Figure 6).

Figure 6: Establishing that wη (φ) < 1 and w (θ | φ) < 1 [42]
It is this point of the proof that I want to focus on. The lecturer has just finished writing the two preliminary steps on the blackboard (in fact, in Figure 6, you can see him writing the "1" of w (θ | φ) < 1, but rather than continuing with the proof on the blackboard, he interrupts the writing process to formulate what the next steps in the proof will be (Transcript 1):

Transcript 1
Video 1: "Exploit the gap" [43]
In this fragment14), the lecturer is not developing the proof on the board, but rather interrupts the writing process in order to make some remarks to the students. These remarks are both retrospective and prospective, i.e., the lecturer is summarizing what he has just done (showing that the two items are less than one), before projecting what he will do next (construct a Dutch book argument). [44]
The lecturer marks the boundary to the previous episode of writing the proof on the board by starting the utterance with "right" (line 1). "Right" (together with "okay") is one of the typical "formal markers" (TURNER, 1972, p.369) used in classroom lessons or university presentations to indicate a change in activity, i.e., a verbal marker "that works to make boundedness, transition, or punctuation in the course of a lesson" (MACBETH, 1987, p.190; see also PAYNE, 1976, p.38; RENDLE-SHORT, 2000, p.21; MONDADA, 2003, p.70; GREIFFENHAGEN, 2008, p.49). Here, "right" indicates that the lecturer is finishing a particular step (namely to show that A < 1) and is ready to move on to the next step in the proof. The lecturer then summarizes what he has just done, namely shown that "both of those things" are less than one (lines 2-3). As you can see in Transcript 1.1, the lecturer indexes the referents of "those things" by quickly pointing to the two items A15) and B16) in the inequality. Since the items are written on the board, he can point to them directly.

Transcript 1.1 [45]
Following this, the lecturer (retrospectively) provides a reason for demonstrating that "both of those things" are less than one, namely that he will use this fact to construct a "Dutch book argument" (lines 3-4). He explains that he is going to do this by "exploit[ing] this space" (line 4) "between these two quantities" (line 5), where the two quantities are not A and B, but rather the left side of the inequality and the right side of the inequality.17) The lecturer again integrates his words with the symbols on the board. As can be seen in Transcript 1.2, while saying "exploit this space," the lecturer traces the less-than sign between the two quantities (starting at the top right corner, he moves the pen left-downwards to the apex of the less-than sign, before moving the pen right-downwards to the bottom right corner of the sign).

Transcript 1.2 [46]
When previously talking about "those things" (Transcript 1.1; line 2), the lecturer had pointed directly at the two items. However, when talking about "this space" he does not just point at the less-than sign, but rather "traces" it, perhaps because he is not so much identifying the less-than sign itself, but rather identifies the less-than sign as the space that has to exist between the two quantities to the left and right of the less-than sign. The lecturer provides even further (visual) elaboration of where "this space" is, by quickly pointing to the "two quantities" between which "this space" is (see Transcript 1.3). Having just traced the less-than sign, he points to the first quantity, namely the two items on the left side of the less-than sign (connecting them within a sort of "lasso" movement), and then points to the second quantity, the item on the right side of the less-than sign.

Transcript 1.3 [47]
It is illuminating to compare how the lecturer refers to the two items on the left side on the inequality in line 2 (Transcript 1.1) and line 5 (Transcript 1.3). In the first case, he uses his pointing gesture to indicate that he is talking about these two items as individual and distinct items. That is to say, having pointed to the first item, he withdraws the pen before pointing to the second item. In contrast, in the second case, the pen stays close to the board when the lecturer moves from the first to the second item, thereby indicating that the two items are here to be seen as parts of one and the same quantity. In other words, the lecturer seems to gesturally express the mathematical distinction between treating the two items on the board as either one or two quantities. [48]
The lecturer has so far talked about things that are directly visible on the board. However, when formulating how they are going to construct the Dutch book argument (lines 5-11), he has to talk about numbers that are not yet on the board. The lecturer first tells the students what these numbers will be used for, namely that these are numbers "with respect to which we're going to bet" (lines 6-7), and then starts to locate these numbers. Since these new numbers are not actually written on the board, he cannot point to them directly. However, as it turns out, he can point to them indirectly, namely in relation to things already on the board. [49]
The lecturer characterizes the first new number as "slightly bigger than double you theta given phi" (lines 7-8), i.e., as slightly bigger than A, the first item on the board. In Transcript 1.4, we can see how the lecturer makes visible this verbal formulation by using his body and by pointing to items on the blackboard. While saying "slightly bigger," he crouches down (portrayed above the verbal utterance in the transcript), and when uttering "double you theta given phi," he moves his hand holding the pen, which had been hovering directly over the middle of that item, to the top right corner of it (portrayed below the verbal utterance in the transcript).

Transcript 1.4 [50]
This episode is a perspicuous example of the interplay of verbal utterances, gesture and body movements, and the symbols on the board.18) The lecturer is talking about a new number that is "slightly bigger" than the first item on the board. He visually articulates that this new number is "bigger" than the item on the board by pointing above and to the right of the item, the natural place on the board to articulate that the new number is bigger than the item on the board. However, not "any" bigger number will do. The new number can only be "slightly" bigger, which the lecturer embodies by making himself smaller, i.e., by "crouching down." The lecturer's hand/pen is visually articulating "bigger," while his body is embodying "slightly." [51]
The second new number is "slightly bigger than doubleyou eta phi" (lines 8-9), i.e., slightly bigger than B, the second item on the board. In Transcript 1.5, we see that this second new number is visually articulated in a similar fashion to the first new number, albeit in a less elaborate manner. The lecturer points to the top right corner of the second item in order to indicate that the new number will be bigger than that number, but the "crouching down" movement (to visually articulate the "slightly") is done much more quickly.

Transcript 1.5 [52]
Although the first two new numbers could not be directly pointed at on the board, they could be located in relation to items on the board (to which they were "slightly bigger"). The third new number is even more difficult to locate. This number has to be chosen so that (a) it is bigger than the product of the two new numbers ("such that their product is less than something," lines 9-10) and (b) smaller than C, the quantity to the right of the less-than sign ("which is slightly less than this," lines 10-11). That is to say, while the first two new numbers had one condition to fulfill, this third new number has two conditions to fulfill.

Transcript 1.6 [53]
In Transcript 1.6, we see the lecturer starting to talk about this third new number by saying that "their [the two new numbers just indicated] product is less than something" (lines 9-10). This "something" is enacted by the lecturer through drawing circles "in the air" (portrayed above the verbal utterance in the transcript). It is important to note that these circles are not drawn anywhere in the air, but directly above the less-than sign (i.e., exactly where in line 4, Transcript 1.2, the lecturer had talked about "exploit this space"). Having uttered "something," the lecturer initiates a self-repair ("uh"), replacing "something" by "zed" (still line 10). While doing so, he draws another circle "in the air," thereby indicating that he is still talking about the same "something," but that this something is now called "zed." He then specifies that this "zed" "is slightly less than this" (lines 10-11), where "this" refers to the item to the right of the less-than sign. Whereas with the first two new numbers the lecturer made visible the fact that these numbers were "slightly bigger," he now visually articulates the fact that the third new number is "slightly less": firstly, just before saying "slightly" he goes down a little; and, secondly, while saying "less than," he moves his pen below the third item (portrayed below the verbal utterance in the transcript). Again, this seems to be a "natural" place to point to: just as the lecturer had pointed above and to the right of an item to indicate "bigger," so now he points below the item to indicate "less." The lecturer places his hand and body physically below the item thereby embodying "less." [54]
The location of this third new number is more elaborate than that of the first two new numbers. The third number is introduced as a "something" that is bigger than the first two new numbers (lines 9-10). If that were the only condition for this "something" (the third new number), then not much more would have to be done. However, the lecturer intends to specify a further condition for this "something." In order to do so, he needs, in a certain sense, to give this "something" a manifestation in order to make clear that what he will say next will still refer to the same "something" that he has been talking about. This manifestation is done on two levels: firstly, the lecturer draws several circles above the less-than sign, thereby locating this "something" (indirectly) in relation to an item on the board; secondly, he gives this "something" a name: "zed shall we say" (line 10). It is quite significant that only this third new number gets a name and this might have to do with the fact that the first two new numbers could be located quite easily through reference to items on already on the board (in fact, the lecturer left a small "dot" to the top right corner of A when locating the first new number). The third new number is bigger than the two new numbers that are not on the board and furthermore has to fulfill two conditions. So there is a danger that the lecturer might not be able to "hold onto it." By giving it a name, the item gains additional substance and makes it easier to formulate two conditions that the item has to fulfill. [55]
Having located the three new numbers "with respect to which we are going to bet," the lecturer turns towards the class and provides a short summary of what they are going to do: "in other words we gonna exploit the gap" (line 11), moving his hands first inwards and then outwards (Transcript 1.7).

Transcript 1.7 [56]
The lecturer is embodying that they are "gonna exploit gap" (where, it should be noted, the bodily aspects occur slightly before the verbal formulation; cf. KENDON, 1980; SCHEGLOFF, 1984): he animates "squeezing" something into a gap by first making himself smaller (moving the head downwards and the shoulder inwards) and then making himself bigger (moving the arms away from the body). It is only at this point that the lecturer finally provides "the reason that we need to start off by showing that both of those things […] are less than zero" (lines 1-3). In lines 11-16, he explains that it is only possible to take numbers that are "slightly bigger" than the two numbers A and B on the board, if those two numbers are not equal to one. That is to say, since all the numbers discussed here represent a probability, they have to lie between 0 and 1; but if, say, number A were equal to 1, then it would not be possible to take a number bigger than A (since that number would have to be bigger than 1, but then it could not represent a probability anymore). [57]
This concludes the episode and the lecturer resumes writing the proof on the board, a transition that is again marked through formal markers ("okay so," line 16). Figure 7 displays what the lecturer subsequently writes on the board:

Figure 7: The three new numbers [58]
This written formulation provides a formal translation into technical notation of what the lecturer has just said in a vernacular way19):
the first inequality, x > w (θ | φ), is the formal translation of the vernacular formulation that the first new number should be bigger than the first item on the board;
the second inequality, y > wη (φ), is the formal translation of the vernacular formulation that the second new number should be bigger than the second item on the board;
the fourth inequality, xy < z, is the first requirement for the third new number, which is supposed to be bigger than the product of the first two new numbers;
and the third inequality, z < (θ ∧ φ), is the formal translation of the second requirement for the third new number, which is supposed to be less than the third item on the board. [59]
The two formulations, the first embodied and vernacular and the second formal and notational, are in a certain sense equivalent. The writing on the board captures what the lecturer has just said and done in the episode. Of course, there are important differences between the two. The embodied formulation is in a certain sense more "vivid" and "intuitive": it visually articulates the new numbers in relation to the items on the board, and also captured the main "idea" of "exploiting the gap." This "idea" is more difficult to see in the written formulation, which, however, has the important advantage over the verbal formulation, in that it can be read outside the context in which it was produced by anyone who knows the mathematical language. The written formulation is thus an example of what LATOUR (1986) has termed "immutable mobiles." [60]
2.3.3 What does this fragment tell us about (professional) mathematics?
I have discussed only one aspect of a short fragment of a lecturer demonstrating a proof at the blackboard. Although I think it is important to resist what WITTGENSTEIN refers to as our "craving for generality" (WITTGENSTEIN, 1969, p.18; cf.; STENLUND, 2002), I do think we can draw at least two tentative conclusions from this discussion. [61]
(1) The first has to do with the general picture of mathematics. It has frequently been remarked that the products of mathematical activities, the written proofs published in books and journals, have a very formal and abstract character. In modern parlance, mathematical proofs seem to resemble the code of computer programs, which may suggest that doing mathematics is analogous to the algorithmic functioning of a machine. In fact, some have adopted the position of what we might call "philosophical formalism," according to which mathematics is simply the manipulation of meaningless symbols according to some abstract rules:
"[Formalism is] [t]he position that mathematics consists merely of formal symbols or expressions which are manipulated or combined according to preassigned rules or agreements. Formalism makes no inquiry as to the meaning of the expressions." (DAVIS & HERSH, 1981, p.413) [62]
It is not clear whether anyone actually holds this view. It is sometimes attributed to Hilbert, but it is highly debatable whether Hilbert himself held to such a crude formalistic view of mathematics (cf., SMORYNSKI, 1988; SIEG, 1999; CORRY, 2006). In any case, by looking at one example of someone actually doing mathematics, namely demonstrating a particular proof to a student audience, it quickly becomes clear that there is nothing "meaningless" or "mechanical" about doing mathematics. Mathematics can be said to be an "abstract" activity in the sense that it typically works with symbols rather than with more concrete things (plants, people, buildings), but the way that the lecturer talks about these abstract symbols is not itself an "abstract" activity, but very much an embodied, situated one. Furthermore, it may perhaps be surprising how many vernacular formulations are at play in the demonstration of the mathematical reasoning: "slightly," "bigger," "less than," "gap," "exploit." Without going so far as to say that mathematics grows out of a number of clearly defined basic metaphors (cf., LAKOFF & NUNEZ, 2000), this fragment nevertheless points to the continuous relevance of vernacular ways of speaking and thinking in doing advanced mathematics. [63]
(2) The second issue that this fragment points to has to do more explicitly with the fact that it was an episode in which the lecturer momentarily interrupts the written exposition of the proof on the blackboard. The lecturer presents what I think could be called the idea ("proof idea," "key idea") of what will be done next. While it is clearly the case that proofs in mathematics have a step-by-step character, these steps are not a homogeneous, linear sequence, but rather are often understood to formulate a (number of) key idea(s):
"A proof isn't any set of deductions: it is a set of deductive links that has coherence and direction. That coherence and direction come from the reasoner having some underlying plan. There must be an idea behind the proof. […] The proof idea can provide the basis for the intuitive understanding of a proof—that is, the flash of insight that can run ahead of the step-by-step articulation of the deductive reasoning. That is how it guides and organizes the individual steps." (BARNES, BLOOR & HENRY, 1996, p.195) [64]
The existence, let alone importance, of key ideas is rarely mentioned in the philosophy or sociology of mathematics (but see POLANYI, 1958; MARKOWITSCH, 1997). However, when analyzing the videos of graduate lectures in mathematical logic, one quickly sees that lecturers frequently explicitly formulate the idea behind a particular proof or part of a proof. These formulations typically occur before doing the proof more formally on the blackboard. Here are two more examples of a lecturer giving a verbal formulation of the idea of the next sequence of steps—before actually writing the proof on the blackboard:
"now at this point (1.0) as I indicated last time (.) there will be in general lots of valuations satisfying that (.) so you gotta cut them down (.) so the idea of- (.) >the way of cutting them down (.) so you can actually pick one (.) cos it's hard to pick one if there's lot >too many of things (.) uhm (.) the way we gonna cut it down (.) is by extending this (.) in fact (.) to a maximal consistent (.) uhm (.) set"
"and now we are going to do something quite interesting (.) we are going to consider (0.5) uh (1.0) a whole lot of inequalities like this (,) uhm (1.0) add them all up in a certain way (.) a:nd (.) get a contradiction" [65]
By formulating the key idea before giving the written formulation, the lecturer not only provides a typical pedagogic orientation device (first tell them what you are going to do; then do it), but also enhances the chances for students to see the mathematical point of the sequence of steps. That is to say, if the lecturer were simply to write down the steps on the blackboard (i.e., in the fragment under discussion immediately write down what is captured in Figure 7), it would be very difficult to see the reasoning behind these steps. By formulating the idea in advance, the lecturer is providing grounds for the students to see why things are done in a particular way. Key ideas frequently seem to be formulated in a relatively vernacular manner (here; "exploit the gap"). As MARKOWITSCH (1997, p.51; my translation) puts it: "A proof idea is rarely expressed by pointing to a particular point in a formal-explicit proof. Rather, proof ideas are vernacularly expressed: through words, diagrams, or gestures." It may be that it is in terms of these "key ideas" that mathematicians remember proofs. That is to say, no mathematician exhaustively remembers the literal wording of a proof that he or she may have read in a book or journal. Rather, mathematicians typically remember the main elements that would allow them to reconstruct a proof (given enough time)—where those main elements are often precisely these "key ideas" (which may, if they are very noteworthy, even get a special name, e.g., "Gödel numbering"). [66]
3. Conclusion: Video Analysis of Mathematical Practice?
Over the last few decades, a number of researchers have tried to demonstrate that there are no reasons to exclude the content of science from sociological investigation. While there is relatively broad consensus that there are no "in principle" reasons preventing sociologists from studying science, it nevertheless remains a challenge to find ways of actually doing so. In other words, researchers are still struggling to find ways to "open up" the natural science and mathematics for sociological studies. [67]
For the experimental sciences, the two most common strategies that have emerged are studies of scientific controversies (where scientists explicitly quarrel over what constitutes "correct" scientific procedure) and studies of laboratory practices (where scientists work collaboratively and in talking to each other provide the researcher, as an onlooker, access to what kind of issues scientists are concerned with). Judging from the number of available studies, it seems that it is even more difficult to open up professional mathematics for sociological investigation than the various experimental sciences. The challenge for researchers, then, is to find ways through which advanced mathematical competences become visible, i.e., amenable for sociological study. [68]
LIVINGSTON's "demonstrative sociology" is one attempt to do so. LIVINGSTON's data are, in a sense, the mathematical proofs themselves. However, LIVINGSTON does not study the proofs as static, textual objects, but rather uses his own competence to instruct readers how to read the proofs themselves, thereby highlighting the seen but unnoticed features in mathematical reasoning. My own "video ethnography" of mathematical lectures is almost a natural extension of LIVINGSTON's study. While in LIVINGSTON's case it is the researcher (LIVINGSTON himself) who is making the mathematical reasoning visible, in the case of the lectures it is the mathematician (the lecturer) who is doing so in a natural setting, in the first place for the students, but thereby also for the researcher. In other words, while LIVINGSTON has to create the visibility of mathematical competence (since his starting objects are the proofs themselves, which have to be "brought to life"), the mathematical lecture is a setting in which mathematical competence is already visibly performed. [69]
This feature of mathematical lectures makes them a great setting for exploiting the advantages of using video to record and preserve the interaction for subsequent analysis. As demonstrated in the various video-based workplace studies, the ability to "go back to" and "go back over" what took place allows the researcher to uncover the taken-for-granted, seen but unnoticed, elements of professional work. In the case of mathematics, it allows us to make visible the features that are, as ROTA (1997, p.184) puts it, not "talked about" in the formal presentation of proofs. [70]
In fact, the ability to record and preserve the mathematical work facilitates output that addresses the inherent weakness in LIVINGSTON's approach, namely that while he can quite successfully deliver a demonstrative sociology of mathematics of basic (high school level) mathematical proofs and problems, the approach fails as a means of approaching more complex (e.g., graduate level) proofs and problems. While the use of video does not guarantee that every reader is therefore able to gain complete technical access to the mathematical reasoning in a particular fragment (e.g., the one discussed in this paper), the reader is nevertheless brought into the presence of mathematicians who do have technical access, and visibly do. In other words, while readers no longer are necessarily able to do the proofs themselves, they can observe mathematicians doing so. [71]
In that sense, my "video ethnography" tries to follow MERZ and KNORR-CETINA's "e-mail ethnography," which explicitly tried to adapt the laboratory study approach for theoretical physics. Since the scientists studied by MERZ and KNORR-CETINA did not work together in a laboratory or office, it was not possible to conduct a simple observational study. However, MERZ and KNORR-CETINA exploited the fact that these scientists collaborated through e-mail exchange and in that exchange explicated their reasoning, in the first place to each other, but thereby also to the researcher (who occasionally needed the help of some clarifying discussion with one of the scientists). The two field sites, graduate lectures and doctoral supervision, were chosen as an extension of MERZ and KNORR-CETINA's strategy of finding situations where reasoning is visibly performed. [72]
In sum, video clearly is no panacea. As WATSON (1999, p.57) warns: "Video-data can, then, be used to illustrate spurious arguments and false problems: such data forms are not necessarily superior to others and may indeed deceive through their apparently persuasive power." When using video, much depends on the setting that is recorded, the questions that are asked of the recordings, and the conceptual approach that informs the analysis. However, by choosing the situation carefully, video data can be a powerful tool to "open up" the details of scientific and mathematical practice. More exciting work remains to be done. [73]
I am immensely grateful to the lecturers and students who allowed me to observe and record the lectures and who more generally helped with the research. Earlier versions of this paper were presented at the European Science Foundation Workshop on Visual Methods, "Qualitative Analysis of Visual Data" (Berlin, September 17-20, 2007), a Boston University Sociology Colloquium (Boston, April 16, 2008), and a LinCS Seminar, University of Gothenburg (Gothenburg, May 22, 2008). I would like to thank all those who gave such helpful and interesting comments and criticisms of the paper when it was presented. I would also like to thank Jac EKE, Wes SHARROCK, Rod WATSON, Martina MERZ, and Philippe SORMANI for their helpful comments and ideas. I gratefully acknowledge the support of the British Academy through a Postdoctoral Fellowship and a Small Research Grant.
1) LYNCH (1993, Chapter 2) argues that such readings of MANNHEIM (and MERTON) exaggerate the differences between the "old" sociology of science and the "new" sociology of scientific knowledge. <back>
2) For an excellent introduction to KUHN's ideas see SHARROCK and READ (2002); KUHN's views on the nature of "conceptual change" are discussed in GREIFFENHAGEN and SHERMAN (2008). <back>
3) In a tertiary system, we count in the following way: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, … In other words, 11 in a tertiary system equals 4 in the decimal system. <back>
4) It is not clear whether this conventional character of mathematics is enough to characterize mathematics as "relative" (see GREIFFENHAGEN & SHARROCK, 2006). <back>
5) Reprinted with permission of Indiana University Press. <back>
6) Reprinted with permission of Indiana University Press. <back>
7) While LIVINGSTON himself uses the term "demonstrative sociology" to describe his work, "e-mail ethnography" is my way of summarizing MERZ and KNORR-CETINA's approach. <back>
8) Theoretical physics, like various branches of mathematics, can be characterized as "theoretical" (or "mathematical") rather than "experimental" work, which is why I include their study in this review. <back>
9) In gambling, a Dutch book is a set of odds and bets, which guarantees a profit, regardless of the outcome of the gamble. Within inductive logic, this is given a more technical definition and a (conditional) belief function w is called "fair," if it is not possible to construct a (conditional) Dutch book against it.
Theorem 1.9 states that every fair conditional belief function is a probabilistic conditional belief function. This is a generalization of Theorem 1.8, which states every fair "simple" belief function w (⋅) is a probabilistic belief function. <back>
10) Starting with w (⋅ | ⋅) and taking any tautology η (e.g., p→p), we define wη (θ) := w (θ | η), where θ is any sentence of the language. From previous results it follows that wη (·) is both fair and a probabilistic belief function. In order to prove that w (⋅ | ⋅) is probabilistic, it therefore suffices to show that the equation holds (where θ and φ are any sentences of the language). <back>
11) A = w (θ | φ), B = wη (φ), and C = wη (θ ∧ φ). <back>
12) That is, wη (φ) < 1. <back>
13) That is, w (θ | φ) < 1. <back>
14) Almost all the mathematics lectures that I have attended over the years have been characterized by a relative absence of questions asked by students and questions asked by lecturers of students. In other words, there is very little "interaction" between lecturer and students, which makes a mathematical lecture in a certain sense a monologue. This is the reason why both the transcript and the analysis focus exclusively on the conduct of the lecturer. Of course, this monologue is nevertheless recipient-designed for a student audience. Although the students do not sit completely still during the lecture, but are writing, listening, or looking at various places (e.g., the board, the lecturer, or their notes), there is an absence of clearly discernible "reactions" to what the lecturer is doing. This makes it difficult for the analyst (and the lecturer) to gain access to how students are analyzing the lecturer's demonstrations.
Other conversation analytic studies of activities that are performed before an audience have exploited the overt behavior of the audience as a basis for the analysis. For example, studies of political speeches (e.g., ATKINSON, 1984; HERITAGE & GREATBATCH, 1986) have used the clapping and booing of the audience as an indicator of how the audience is analyzing the speech. In the graduate lectures of mathematical logic, I have so far been unable to find similar signals produced by the students, which makes it difficult to study in which ways the students are orienting to what the lecturer is doing. <back>
15) w (θ | φ). <back>
16) wη (φ). <back>
17) That is, the first quantity is w (θ | φ) · wη (φ) and the second quantity is wη (θ ∧ φ). <back>
18) KNOBLAUCH (2008, p.84) discusses a similar example, taken from Powerpoint presentations, where "gesture, talk, and slide seem to elucidate one another respectively." <back>
19) See SCHNETTLER (2006, p.164) for a discussion of how, in the case of Powerpoint presentations, the speaker "translates" the visual slide into a verbal commentary. <back>
Atkinson, J. Maxwell (1984). Our masters' voices: The language and body language of politics. London: Methuen.
Barnes, Barry; Bloor, David & Henry, John (1996). Scientific knowledge: A sociological approach. London: Athlone.
Bloor, David (1976). Knowledge and social imagery. London: Routledge and Kegan Paul.
Bloor, David (1994). What can the sociologist of knowledge say about 2 + 2 = 4? In Paul Ernest (Ed.), Mathematics, education and philosophy: An international perspective (pp.21-32). London: Falmer.
Collins, Harry M. & Pinch, Trevor J. (1993). The golem: What everyone should know about science. Cambridge: Cambridge University Press.
Corry, Leo (2006). Axiomatics, empiricism, and Anschauung in Hilbert's conception of geometry: Between arithmetic and general relativity. In José Ferreirós & Jeremy J. Gray (Eds.), The architecture of modern mathematics: Essays in history and philosophy (pp.133-156). Oxford: Oxford University Press.
Davis, Philip J. & Hersh, Reuben (1981). The mathematical experience. Boston: Birkhäuser.
Garfinkel, Harold (1967). Studies in ethnomethodology. Englewood Cliffs, NJ: Prentice-Hall.
Garfinkel, Harold (2002). Ethnomethodology's program: Working out Durkheim's aphorism. Lanham, MD: Rowman & Littlefield.
Garfinkel, Harold & Sacks, Harvey (1970). On formal structures of practical action. In John C. McKinney & Edward A. Tiryakian (Eds.), Theoretical sociology: Perspectives and developments (pp.338-366). New York: Appleton-Century-Crofts.
Goodwin, Charles (1994). Professional vision. American Anthropologist, 96(3), 606-633.
Goodwin, Charles (1995). Seeing in depth. Social Studies of Science, 25(2), 237-274.
Goodwin, Charles & Goodwin, Marjorie Harness (1996). Seeing as situated activity: Formulating planes. In Yrjö Engeström & David Middleton (Eds.), Cognition and communication at work (pp.61-95). Cambridge: Cambridge University Press.
Greiffenhagen, Christian (2008). Unpacking tasks: The fusion of new technology with instructional work. Computer Supported Cooperative Work (CSCW), 17(1), 35-62.
Greiffenhagen, Christian & Sharrock, Wes (2006). Mathematical relativism: Logic, grammar, and arithmetic in cultural comparison. Journal for the Theory of Social Behaviour, 36(2), 97-117.
Greiffenhagen, Christian & Sherman, Wendy (2008). Kuhn and conceptual change: On the analogy between conceptual changes in science and children. Science & Education, 17(1), 1-26.
Heath, Christian & Luff, Paul (1992). Collaboration and control: Crisis management and multimedia technology in London underground line control rooms. Computer Supported Cooperative Work (CSCW), 1(1-2), 69-94.
Heath, Christian & Luff, Paul (2000). Technology in action. Cambridge: Cambridge University Press.
Heritage, John & Greatbatch, David (1986). Generating applause: A study of rhetoric and response at party political conferences. American Journal of Sociology, 92(1), 110-157.
Heritage, John C. & Watson, Rod (1979). Formulations as conversational objects. In George Psathas (Ed.), Everyday language: Studies in ethnomethodology (pp.123-162). New York: Irvington.
Heritage, John C. & Watson, Rod (1980). Aspects of the properties of formulations in natural conversations: Some instances analysed. Semiotica, 30(3/4), 245-262.
Hill, Richard J. & Crittenden, Kathleen Stones (Eds.) (1968). Proceedings of the Purdue symposium on ethnomethodology. Institute for the Study of Social Change, Department of Sociology, Purdue University.
Hindmarsh, Jon & Heath, Christian (2000). Sharing the tools of the trade: The interactional constitution of workplace objects. Journal of Contemporary Ethnography, 29(5), 523-562.
Kendon, Adam (1980). Gesticulation and speech: Two aspects of the process of utterance. In Mary Ritchie Key (Ed.), The relationship of verbal and nonverbal communication (pp.207-227). The Hague: Mouton.
Knoblauch, Hubert (2008). The performance of knowledge: Pointing and knowledge in Powerpoint presentations. Cultural Sociology, 2(1), 75-97.
Knoblauch, Hubert; Schnettler, Bernt; Raab, Jürgen & Soeffner, Hans-Georg (Eds.) (2006). Video analysis: Methodology and methods. Frankfurt am Main: Peter Lang.
Knorr-Cetina, Karin (1981). The manufacture of knowledge: An essay on the constructivist and contextual nature of science. Oxford: Pergamon.
Kuhn, Thomas S. (1962/1996). The structure of scientific revolutions (third edition). Chicago: University of Chicago Press.
Lakatos, Imre (1976). Proofs and refutations: The logic of mathematical discovery (edited by J. Worrall and E. Zahar). Cambridge: Cambridge University Press.
Lakoff, George & Nunez, Rafael (2000). Where mathematics comes from: How the embodied mind brings mathematics into being. New York: Basic Books.
Latour, Bruno (1986). Visualization and cognition: Thinking with eyes and hands. Knowledge and Society, 6, 1-40.
Latour, Bruno (2005). Reassembling the social: An introduction to actor-network-theory. Oxford: Clarendon.
Latour, Bruno & Woolgar, Steve (1979). Laboratory life: The social construction of scientific facts. Beverly Hills: Sage.
Lindwall, Oskar & Lymer, Gustav (2008). The dark matter of lab work: Illuminating the negotiation of disciplined perception in mechanics. Journal of the Learning Sciences, 17(2), 180-224.
Livingston, Eric (1986). The ethnomethodological foundations of mathematics. London: Routledge and Kegan Paul.
Livingston, Eric (1987). Making sense of ethnomethodology. London: Routledge and Kegan Paul.
Livingston, Eric (1995). An anthropology of reading. Bloomington, IN: Indiana University Press.
Livingston, Eric (1999). Cultures of proving. Social Studies of Science, 29(6), 867-888.
Livingston, Eric (2006). The context of proving. Social Studies of Science, 36(1), 39-68.
Lynch, Michael (1985). Art and artifact in laboratory science: A study of shop work and shop talk in a research laboratory. London: Routledge and Kegan Paul.
Lynch, Michael (1993). Scientific practice and ordinary action: Ethnomethodology and social studies of science. Cambridge: Cambridge University Press.
Lynch, Michael & Macbeth, Douglas H. (1998). Demonstrating physics lessons. In James G. Greeno & Shelley V. Goldman (Eds.), Thinking practices in mathematics and science learning (pp.269-297). Mahwah, NJ: Lawrence Erlbaum.
Macbeth, Douglas H. (1987). Managements' work: The social organization of order and troubles in secondary classrooms. Ph. D. thesis, University of California, Berkeley.
Macbeth, Douglas H. (1990). Classroom order as practical action: The making and un-making of a quiet approach. British Journal of Sociology of Education, 11(2), 189-214.
MacKenzie, Donald A. (1999). Slaying the Kraken: The sociohistory of a mathematical proof. Social Studies of Science, 29(1), 7-60.
MacKenzie, Donald A. (2001). Mechanizing proof: Computing, risk, and trust. Cambridge, MA: MIT Press.
Mannheim, Karl (1936). Ideology and utopia: An introduction to the sociology of knowledge. London: Routledge and Kegan Paul.
Markowitsch, Jörg F. (1997). Metaphysik und Mathematik: Über implizites Wissen, Verstehen und die Praxis in der Mathematik. Ph.D. thesis, University of Vienna.
Merz, Martina (1998). "Nobody can force you when you are across the ocean"—face to face and e-mail exchanges between theoretical physicists. In Crosbie Smith & Jon Agar (Eds.), Making space for science: Territorial themes in the shaping of knowledge (pp.313-329). Basingstoke: Macmillan.
Merz, Martina & Knorr-Cetina, Karin (1997). Deconstruction in a "thinking" science: Theoretical physicists at work. Social Studies of Science, 27(1), 73-111.
Mondada, Lorenza (2003). Working with video: How surgeons produce video records of their actions. Visual Studies, 18(1), 58-73.
Mondada, Lorenza (2007). Operating together through videoconference: Members' procedures for accomplishing a common space of action. In Stephen Hester & David Francis (Eds.), Orders of ordinary action: Respecifying sociological knowledge (pp.51-67). Aldershot: Ashgate.
Payne, George C. F. (1976). Making a lesson happen: An ethnomethodological analysis. In Martyn Hammersley & Peter Woods (Eds.), The process of schooling: A sociological reader (pp.33-40). London: Routledge and Kegan Paul.
Pickering, Andrew (1995). The mangle of practice: Time, agency, and science. Chicago: University of Chicago Press.
Polanyi, Michael (1958). Personal knowledge: Towards a post-critical philosophy. Chicago: University of Chicago Press.
Pólya, George (1945). How to solve it. Princeton: Princeton University Press.
Rav, Yehuda (1999). Why do we prove theorems? Philosophia Mathematica, 7(1), 5-41.
Rendle-Short, Johanna (2000). When "okay" is okay in computer science seminar talk. Australian Review of Applied Linguistics, 22(2), 19-33.
Rota, Gian-Carlo (1997). The phenomenology of mathematical proof. Synthese, 111(2), 183-196.
Sacks, Harvey (1992). Lectures on conversation (edited by Gail Jefferson). Oxford: Blackwell.
Schegloff, Emanuel A. (1984). On some gestures' relation to talk. In J. Maxwell Atkinson & John Heritage (Eds.), Structures of social action: Studies in conversation analysis (pp.266-296). Cambridge: Cambridge University Press.
Schegloff, Emanuel A. (2007). Sequence organization in interaction. Cambridge: Cambridge University Press.
Schnettler, Bernt (2006). Orchestrating bullet lists and commentaries: A video performance analysis of computer supported presentations. In Hubert Knoblauch, Bernt Schnettler, Jürgen Raab & Hans-Georg Soeffner (Eds.), Video analysis: Methodology and methods (pp.155-169). Frankfurt am Main: Peter Lang.
Shapin, Stevin & Shaffer, Simon (1985). Leviathan and the air-pump: Hobbes, Boyle, and the experimental life. Princeton: Princeton University Press.
Sharrock, Wes & Ikeya, Nozomi (2000). Instructional matter: Readable properties of an introductory text in matrix algebra. In Stephen Hester & David Francis (Eds.), Local educational order: Ethnomethodological studies of knowledge in action (pp.271-288). Amsterdam: John Benjamins.
Sharrock, Wes & Read, Rupert (2002). Kuhn: Philosopher of scientific revolution. Oxford: Polity.
Sieg, Wilfried (1999). Hilbert's programs 1917–1922. Bulletin of Symbolic Logic, 5(1), 1-44
Smorynski, C. (1988). Hilbert's programme. CWI Quarterly, 1(4), 3-59.
Stenlund, Sören (2002). The craving for generality. Revista Portugesea de Filosofia, 58(3), 569-580.
Turner, Roy (1972). Some formal properties of therapy talk. In David Sudnow (Ed.), Studies in social interaction (pp.367-396). New York: Free Press.
Watson, Rod (1998). Ethnomethodology, consciousness and self. Journal of Consciousness Studies, 5(2), 202-223.
Watson, Rod (1999). Driving in forests and mountains: A pure and applied ethnography. Ethnographic Studies, 4, 50-60.
Weber, Keith (2001). Student difficulty in constructing proofs: The need for strategic knowledge. Educational Studies in Mathematics, 48(1), 101-119.
Wittgenstein, Ludwig (1969). The blue and brown books (second ed.). Oxford: Basil Blackwell.
Videos
Video_1: http://medien.cedis.fu-berlin.de/stream01/cedis/fqs/3-09/greiffenhagen.flv (425 x 355)
Christian GREIFFENHAGEN is a British Academy Postdoctoral Fellow at the University of Manchester, currently conducting ethnographic research on mathematical practice, which aims to address a key challenge for the sociology of scientific knowledge: What could a sociology of mathematics look like? His doctoral research (at the University of Oxford) was a video-based ethnographic study of how a new innovative storyboarding software embedded in everyday classroom practice and how this reconfigured classroom interaction. His recent publications are "Unpacking tasks: the fusion of new technology with instructional work," Computer Supported Cooperative Work (CSCW), "Where do the limits of experience lie? Abandoning the dualism of objectivity and subjectivity," History of the Human Sciences (with Wes SHARROCK), and "School mathematics and its everyday other? Revisiting Lave's 'Cognition in Practice'," Educational Studies in Mathematics (with Wes SHARROCK).
Contact:
Christian Greiffenhagen
School of Social Sciences
Arthur Lewis Building
University of Manchester
Manchester M13 9PL
UK
E-mail: christian.greiffenhagen[replace_with_at]manchester.ac.uk
URL: http://www.socialsciences.manchester.ac.uk/disciplines/sociology/about/staff/greiffenhagen/
Greiffenhagen, Christian (2008). Video Analysis of Mathematical Practice? Different Attempts to "Open Up" Mathematics for Sociological Investigation [73 paragraphs]. Forum Qualitative Sozialforschung / Forum: Qualitative Social Research, 9(3), Art. 32, http://nbn-resolving.de/urn:nbn:de:0114-fqs0803323.