

Volume 12, No. 1, Art. 31 – January 2011
Researching Living/Lived Mathematical Work
Wolff-Michael Roth
Abstract: In qualitative research, accounts of experience are often taken for the experience itself despite ample phenomenological research that has articulated the difference between the living presence and the presence of the present, which requires representation. In this contribution, I provide practical examples that exhibit the difference between two aspects of mathematics that form an irreducible pair: living/lived mathematical work and accounts of mathematical work. Directions for the future practice of research are provided.
Key words: phenomenology; ethnomethodology; mathematics; living work; work accounts
Table of Contents
1. Introduction
2. The Living/Lived Work of Mathematics
2.1 Case 1: What makes a cube a cube?
2.2 Case 2: Proving the angle sum of a triangle
2.2.1 The account
2.2.2 The living/lived work of proving
3. Of Work and Accounts
4. Directions for Research
5. Coda
Qualitative research generally uses interviews to get at the experience that research participants have had some time before being interviewed. HUSSERL (1980 [1928]) however points out that our accounts of experience continually change, refracted by the layers of intervening experiences and times. Moreover, there is a dehiscence in principle between Being (Sein, Être) and the way in which it can be accounted for, i.e., made present again in language, that is, in terms of beings (Seiendes, étant) (HEIDEGGER, 1977 [1950], 2000 [1954]). Is it possible in principle to communicate lived experiences and lived work? In fact, there is. When research articles are constructed such that the reader has to engage in and enact the very work that the paper is about, then the reader experiences the very experiences and work described (GREIFFENHAGEN, 2008). That is, readers are enabled to experience the experience/work when the article constitutes a form of instruction to actually do what brings about the experiences/work. The purpose of this paper is to present examples of accessing lived work and lived experiences without actually having to interview research participants. I do so with examples from mathematics, because it is a domain more likely to be unfamiliar and strange so that readers cannot "naturally" provide explanations that are based on common sense and the "pre-constructed," which looms everywhere and therefore constitutes a stumbling block for doing good empirical work (BOURDIEU, 1992). [1]
In a text that is part of the project of articulating the crisis of the European sciences, HUSSERL (1939) describes how geometry evolved from everyday non-geometrical practices of the early Greek. Rather than being opposite to formal mathematics, the intuitions of the pre-geometrical Greek constitute the foundations and possibilities for formal geometry to emerge. In this paper, a distinction is made between (a) the subjectively experienced lived work of mathematics and (b) the formal, objective written accounts of mathematics. The two are irreducibly tied together to produce geometry as objective science. Without the living/lived work, there is no geometry; without the written accounts, geometry could not be handed down as objective science. Together, the two aspects constitute a Lebenswelt pair. [2]
In research on mathematical experience, HUSSERL's distinction tends not to be heeded. Thus, a frequently cited text entitled "The Mathematical Experience" (DAVIS & HERSH, 1981) only focuses on the second part of HUSSERL's distinction in presenting either mathematical content or biographical experiences. Both are accounts of mathematics and mathematical work rather than the work itself. There is one text, however, that deals with the Lebenswelt pair in study of mathematics in the local production of social order (LIVINGSTON, 1986). The study is concerned with "rediscovering and exhibiting the naturally accountable mathematical proof, in its identifying detail for mathematicians, as a social achievement" (pp.x-xi). The text describes the structures of the lived work of proving and exhibits the transcendental character of this work and of the objects that are the integral and constitutive parts of the resulting proofs. [3]
LIVINGSTON's (1986) text is difficult, as it deals with content inaccessible to most mathematics educators specifically and other educators and social scientists more generally. This limits what the approach can communicate about mathematical practices and lived experiences specifically and about human practices more generally (GREIFFENHAGEN, 2008). The purpose of the present text is to articulate in a more accessible way the difference between the living/lived work of mathematics (mathematical perception) and accounts of this work. Here, I insist on the difference between lived mathematical experience and accounts of mathematical experience. Almost all research, both quantitative and qualitative, is concerned with accounts of mathematical experience rather than with the lived work of mathematics. I articulate the difference between the two and provide some guidance with respect to the ways of going about researching the lived work rather than accounts thereof. In this, I counter the false belief that our experiences are "constructed," and insist that the real work that makes mathematics an objective science is actually lived and the result of our living/lived bodies rather than that of the constructivist mind. Whereas the "ekstatic" aspects of human experience are subject to intersubjective differences, that is, they are "constructed" and "negotiated" in culture, the very nature of the human flesh that produces the experience, the internal and invisible life that actually brings about experience derives from the common structure of Being (HENRY, 2005) and the biological body (VON UEXKÜLL, 1973). In this manner, I state an approach that is an incommensurable, asymmetrical alternate form in relation to formal analyses of living/lived mathematical experience specifically and of living/lived experience more generally. [4]
2. The Living/Lived Work of Mathematics
I begin this investigation with two practical examples, which, when readers engage with these, allows them to live the mathematical experiences of seeing a geometrical object as a specific object (cube) and doing the proof of the angle sum of a triangle. [5]
2.1 Case 1: What makes a cube a cube?
To start our inquiry into the difference between the lived work of mathematics—lived mathematical experience—and an account of mathematical experience, consider the drawing in Figure 1. What do you see? Take a moment to look at the figure and find an answer before you proceed reading.
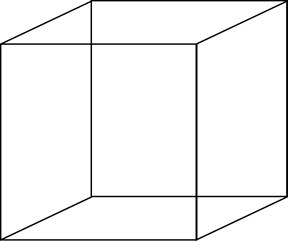
Figure 1: This diagram has been used in psychological research on perception and is known as the Necker Cube. [6]
The figure is known in the psychological research as the Necker Cube. Although there are but a few black lines on a two-dimensional sheet of paper, most research participants report something like "I see a (three-dimensional) cube," "I see a cube from below that extends from front right to back left," or "I see a cube from the top that extends from the front left to the back right." When asked further, participants may outline, moving their fingers along the lines, where they see the different surfaces of the particular cube they see. In their statements—which may be provided verbally alone or communicated using a range of semiotic resources—they provide accounts or reports of experience. What they have not provided us access to is the actual lived work that is obliquely referred to in the account/report. [7]
Qualitative researchers including researchers employing phenomenography tend to be interested in reporting all the different things that research participants have reported seeing, which, in addition to a cube, may simply be a set of lines, or an assembly of several flat geometrical figures, and so on. Constructivist mathematics educators are likely tempted to say that these participants "constructed" the particular cube or cubes that they see. Both sets of research reports are limited, as they do not get us any closer to the real question of the lived work (experience) that is denoted in the reports/accounts that provide us with the structures that people exhibit to one another. So what more is there? This is the question that GARFINKEL (1996) asks, and where he makes the distinction between formal analysis and ethnomethodology. The former approaches report structures whereas the latter is concerned with the lived work that brings the structures about. Generally, ethnomethodology, as its descriptive name suggests, is concerned with the methods by means of which people (Gr. ethnos) produce and exhibit to each other the structures of social action, whereas formal analysis, generally having to specify particular research methods, is concerned with the identification of the structures. [8]
So what is the lived work underlying the report of seeing this or that cube? The drawing in Figure 1 allows us to investigate perception and how we come to see what we see. Upon first sight, you may see a cube, if you see a cube at all, from slightly above extending from the front left to the back and right (Figure A1a). But, if you see a cube, you might actually see one from below and extending from front right to the left back (Figure A1b). These two perceptions are the two spatial configurations that are seen in psychological experiments, where these are categorized as "cognitive illusions." Rather than wondering about illusions, let us engage in the analysis of the lived work of perception to find out what is at the origin of the perception of the cube in one or the other way (i.e., from below or from above). We may do so by, for example, by exploring how to quickly switch back and forth from the cube seen slightly from above to the other one seen from below. [9]
To begin with, look at Figure 1 and allow the first cube to appear, for example, the one that you see from below and extending into the back toward the left and then intend seeing the other one until you see it. Move back to see the first; return to the second. You might also do this: look at the first cube, the one seen from the bottom and extending toward the back and left. Close your eyes—but intend to see the other cube upon opening the eyes again. Practice until you can switch between the two in the rapid flicker of the eyelids. Once you achieve this, observe what is happing with your eyes during the flicker. That is, how can you generate this or that experience voluntarily? [10]
You may notice that if you place your eyes to the lower left corner that appears inside the set of lines and then move toward a non-present vanishing point to the left ("along the surface")—this may be along the edge leading from the "front" vertex toward the back left—then the cube-seen-from-below becomes instantly apparent. Similarly, focusing on the equivalent vertex further up and right and then moving along the edge "backward" to a non-existing vanishing point allows you to see a cube-from-above. That is, unbeknownst to your intellectual consciousness, the movement of the eye from one of the two vertices toward a non-existing vanishing point in the back to the left or right of the diagram creates one or the other perceptual experience. This, therefore, is a statement about how the work of seeing produces the cube even if we do not attend to it. If the eyes do not make these movements, then the cubes do not appear and the lines remain on a flat surface. Most importantly, therefore, this experiment shows us that the cube is not (intentionally) constructed because when you looked at the figure for the first time, the cubes appeared, you did not intentionally construct it. And for the very first time you looked at the figure, you might have not seen any cube at all or only one and not the other. [11]
How do the eyes know to move like this to make the cube appear? The answer extends the possibility of this text, but I have worked out one based on the phenomenology of the flesh (ROTH, 2010, in press). Briefly stated, this knowing emerges from first uncoordinated movements during which the flesh auto-affects itself such that it develops the capacity to move and develops an immanent memory of this capacity. In other words, during first random movements, corporeal-kinetic movement forms (archetypes) emerge that would be more ancient, more basic than any "image schemas" or "sensorimotor schemas," if the latter exist at all (SHEETS-JOHNSTONE, 2009). Nothing is constructed at that point because there are no tools available for the construction; in fact, this capacity, the self-knowledge producing the movement precedes any intentional movement, any intention to act, and any intentional thought. Before I can intentionally move the eyes, these have to immanently know that they can move. [12]
It is clear in the above account of the work that different movements of the eyes underlie the different experiences; that is, different movements produce different experiences. [13]
We can push this analysis further—but this is difficult and requires considerable practice. The question we attempt to answer is this: How do we see one and the same cube over an extended time? Or, equivalently, is the eye movement from the vertex to the corresponding vanishing point necessary for us to see a cube? To reach an answer, fixate, for example, the lower vertex. Or, equivalently, attempt to have both cubes appear at the same time. You may not be able to achieve this feat on your first few attempts—psychologists generally use equipment that allows an image to be fixed on the retina. But as soon as you achieve this feat—that is, the eye fixed so that the image falls on the same spots on the retina—you will notice that the figure dissolves completely and you won't see but a dark grey perceptual field. You no longer see lines. That is, as soon as the eye no longer moves, you cannot see the lines and even less a cube. To see a line or cube, the eye needs to move back and forth between the cube and some other place that constitutes the ground against which the cube appears as the figure. In one sense, the cube is a cube because the eye finds it again upon moving away, and to generate the cube, my eye has to move from the vertex to its corresponding vanishing point. [14]
The upshot of this investigation is this: We do not just see or recognize a cube because its mirror image is produced on the retina. Rather, our eyes have to do work, and associated with this work there are changes on the retina. Based on the changing images, and based on prior experience, we have learned to see cubes. We can see cubes because our eyes know what they have to do to make a cube appear. It is in the non-perceived movement of the eye that the distension and dehiscence between the cubical figure and the ground occurs and that the former comes to detach itself from the latter. But we should not think of the image as something standing before the ground, as if projected against a screen; rather, in the image the ground is rising to us (NANCY, 2003). It is not merely, as enactivist theorists would say, that the organism is bringing forth a world—the world gives itself to the organism, which learns how to make any figure reappear. That is, the movements of the eyes are not random, not constructed, but they are entrained by the structures of the material world in which the organism is embedded. "It is in reference to my flesh that I apprehend the objects in the world" so that "in my desiring perception I discover something like a flesh of objects" (SARTRE, 1956, p.392). It is in reference to my flesh that I apprehend the objects of the world, which means "that I make myself passive in relation to them and that they are revealed to me from the point of view of this passivity, in it and through it" (p.392). There is therefore a fundamentally passive component to perception that tends to be obliterated in the (social, radical) constructivist literature but that is essential to understand the dual, subjective/objective nature of mathematics that has become the point of unresolved contention between formal and constructivist accounts of mathematics. [15]
We can enact further phenomenological investigations relevant to geometry by, for example, investigating the conditions for seeing an angle or seeing two lines as equal or unequal. Thus, in "The Emergence of Geometry as Objective Science in Elementary Classrooms" (ROTH, in press), I exhibit how the movements of the eyes make us see two line segments of demonstrably equal length appear to have different lengths (Figure 2). The MÜLLER-LYER illusion is produced as the eye follows the inward and outward pointing arrows at their ends in a different way. Thus, such a perception of equality of lengths important to perception in geometry is explained by the movements of the eyes in the context of particular configurations of lines. This illusion is sustained even when we have measured the two lines and therefore know that the two lines are of equal length. That is, we are passive with respect to our perception even when "we know better." There is therefore nothing constructive about this experience, it is happening to us. We see what we see because of the movement of the eyes, movements that our eyes, as aspect of our living/lived bodily selves, are given as originary, archetypal corporeal-kinetic forms.
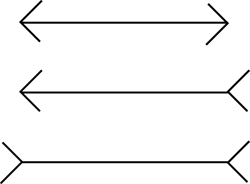
Figure 2: The MÜLLER-LYER "illusion" makes line segments of equal length to be of different length. [16]
We can sum up this first part of our investigation by saying that there are two parts to perception: (a) the account or gloss of what is seen and (b) the living/lived work that underlies the account. Qualitative research generally and phenomenographically oriented qualitative research specifically investigates and reports on these accounts; this kind of research presents us with the structures that either the participants or the researchers report. It is our phenomenological analysis that actually leads us to an understanding the living/lived work that produces the different experiences that people report. For this reason, the two approaches are asymmetrical, incommensurable alternates (GARFINKEL, 2002). [17]
2.2 Case 2: Proving the angle sum of a triangle
In the following description of mathematical practices, using proving as an example, I follow the kind of studies produced in the field of ethnomethodology of mathematics (e.g., LIVINGSTON, 1986, 1987; GREIFFENHAGEN & SHARROCK, 2005, 2008). This work is concerned with the irreducible relation of living/lived work and accounts of this work. These descriptions are consistent with the phenomenological studies of the foundation of mathematics (geometry), which recognize the co- presence of lived (subjective) and formal (objective) dimensions of mathematics (HUSSERL, 1939). Accordingly, there are records and accounts of mathematical proofs, on the one hand, and the living/lived labor of doing a proof, on the other hand. [18]
The proof that the internal angle sum of a triangle is 180° involves the following. In a first step, we note the relationships between angles that are produced when a line crosses two parallel lines (marked by the sign "»").
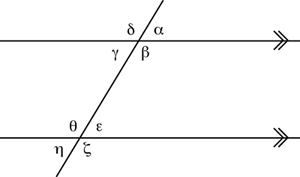
Figure 3: The angles produced when a line crosses two parallel (») lines.
The pairs (α,ε), (β,ζ), (η,γ), and (θ,δ) are known as corresponding angles; corresponding angles are equal (i.e., α=ε, etc.).
The pairs (α,γ), (β,δ), (ε,η), and (ζ,θ) are known as vertically opposite angles; vertically opposite angles are equal (i.e., α=γ, etc.).
The pairs (ε,γ) and (θ,β) are alternate angles. Alternate angles are equal (i.e., ε=γ)—because of (a) and (b). [19]
With these identities in place, we can prove that in the Euclidean plane, the angle sum in a triangle is 180°—if the total angle around a point is defined as 360°. This proof includes the following steps together with the diagrams in Figure 4.
Any triangle can be drawn such that the base lies on one of two parallel lines and the opposing vertex on the other (Figure 3a).
We know that alternate angles are equal, as marked in Figure 3b.
Hence, because of configuration of lines at the upper parallel, that α, β, and γ add up to 180°, that is, α+β+γ= 180°. Therefore three angles in a triangle add up to 180°.
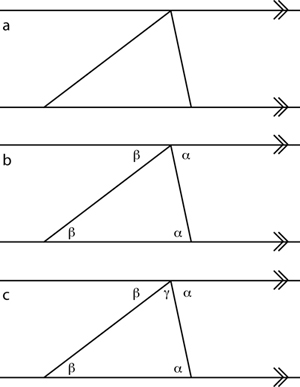
Figure 4: Steps in and part of the account for the proof that the interior angle sum of a triangle is 180° [20]
The preceding steps and figures do not constitute the entirety of the proof; rather, they constitute what we know to be the proof account. These are the parts that one might find in a textbook on geometry, on a website, or, in the case of new mathematical discoveries, in relevant journals. This is the part, therefore, that allows us to re-do the proof over and over again, which certainly has been done so since some time in antiquity, when the proof was done for a first time. For example, the reviewers of an article take the submitted proof as instructions for doing the proof, checking whether there are "no holes" in the proof procedure. In written form, this account suffices to be able to hand the proof procedure down—initially, to share it with others in the prover's community. Ordinarily, newcomers to a discipline learn these practices in face-to-face work with others where monitoring and feedback correct actions; but the written accounts are such that they allow others to re-discover the proof in their own praxis (HUSSERL, 1939).1) This possibility for the rediscovery of the proof in fact constitutes the objective and tradable nature of geometry as objective science. Thus, "the important function of writing is to enable the continual objectivity of ideal sense entities in the curious form of virtuality" (p.212). The ideal (subjective) objects exist virtually in the world in written form, and they therefore can be actually produced at any time. The lived praxis (labor) within which this written account counts as the proof, however, is not contained in the written account. It is precisely this lived work that we are interested in here and in ways of capturing it. The objectivity of mathematics and the sciences derives precisely because of the possibility to reproduce the practices in and through the living/lived work because subjectivity and pathos constitute the essence of community and intelligibility (HENRY, 1990). We already see some of what is involved in the preceding inquiry concerning what makes a cube a cube. To bring this proof to life we actually need to do it in and as of living/lived labor for which the written record has to provide sufficient resources. [21]
2.2.2 The living/lived work of proving
I am interested in the living/lived work within which such accounts constitute the resources that allows us to count what is happening as a proof. Part of the kind of work involved is articulated in the first subsection, that is, the lived work of seeing. In the present instance, for example, this living/lived work includes the re/cognition that pairs of corresponding, opposite, or alternate angles are equal. That these pairs of angles are equal presupposes the seeing of each angle—where the work of seeing is described in Subsection 1.1. Such seeing is related to the living/lived work of drawing multiple lines, each of which bisects the plane (Figure 5). This work involves particular movements, "integral kinaesthetic structures or kinetic melodies" (LURIA, 1973, p.176), which are inscribed in the living/lived body (the flesh). From the perspective of the living/lived work, the writing gesture produces the divisions of our pre-geometrical experience of left/right, up/down, and so on.
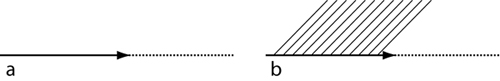
Figure 5: In the dynamic of drawing a line, the plane becomes bisected, here denoted by a hatched and an unhatched part. [22]
When, after the completion of the first line (involving a complete bisection of the plane), a second line is added, it, too, bisects the plane. Four sectors are thereby produced, which appear in three different hatchings: not hatched, once-hatched, and twice-hatched (Figure 6a).
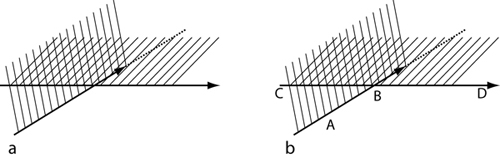
Figure 6: Two intersecting lines produce four sectors. [23]
We could have also drawn the second line in the reverse and produced the same account. For this reason, the angles enclosing the single-hatched areas are the same. What is in the first drawing the angle forming first to the left and then to the right will be, upon beginning the diagram from the other side, again first to the left and then to the right. In this very act of drawing, we also produce an order that goes with the naming of locations (Figure 6b). In this way, the unfolding from the drawing the AB line with respect to CD forms angles ABC and ABD, which we may also name, following the tradition, by the Greek letters α and β (as well as the equivalent angles γ and δ) (Figure 7). Here, the order in the actual making constitutes a conceptual order: "The temporally placed label of an angle or its apparently disengaged placement in a finished figure exhibits this seen relationship as a proof-specific relevance" (LIVINGSTON, 1987, p.96). The conceptual order is in and arises from the movement rather than from the constructive mind, if there is indeed something of that kind. Mind and sensorimotor schema are postkinetic, as are all accounts of mathematical experience.
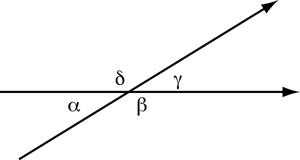
Figure 7: The placement of the labels a and b is apparently disengaged from the temporal practice of drawing the figure. [24]
The relationships between the lines, angles, bisectors, and sectors have to be seen; this seeing, as shown in Subsection 2.1 is based on the movements of the eyes, movements that we are not in conscious control of. Not surprisingly, phenomenological philosophers have recognized the fundamental passivity that is associated with a first cognition that such seeing involves (MARION, 2002). Any first formation of sense, therefore, has two passive moments, the first existing in the first cognition and the second in the fact of the retention of this first cognition (HUSSERL, 1939). Thus,
"the passivity of the initially darkly awakened (insight) and the eventually increasing clarity of that which appears is accompanied by the possibility of a change in the activity of a remembrance, in which the past experience is lived again actively and quasi anew" (p.211). [25]
The memory is awakened passively but can be transformed back into corresponding activity. The recognized relationship may therefore be maintained throughout the proof procedure, which leaves as its end result the sequence of diagrams in Figure 3 and Figure 4. In the drawing, we do not specify a particular angle to be produced. Any work that produces two, non-parallel lines suffices to get us to this point. This fact produces the generality of the proof procedure. [26]
This memory is important in the constitution of geometry as an objective science in and through the subjective, living/lived work of the geometer. A sense-forming act that came about spontaneously can be actively/passively remembered, and therefore reproduced not only by the original individual but by any other individual as well. It is in the reproduction of the living/lived work that the evidence of the identity between original and subsequent act arises (HUSSERL, 1939): "That which now is originally reconstituted is the same as what was evident before" (p.211). That is, together with the original sense formation comes the possibility of an arbitrary number of repetitions that are identical in the chain of repetitions. That is, the very living/lived work that allows me to recognize relationships again make for the social nature of geometry and its historicity as objective science. [27]
Interestingly, the very generality of the proof derives from the way in which the living/lived work unfolds. For example, in the drawing of a line that crosses two parallel lines and labeling alternate angles using the same letter, the proof makes available that any such line could have been drawn, which in fact occurs when the second line between the two parallels is drawn such as to form a triangle. The very possibility to have one line between parallel lines with alternate angles enables all other lines. The relations between the angles in configurations of parallel lines crossed by a third thereby imply the angle sum of the triangle to be 180°. That is, from the way in which living/lived work draws parallel lines and the equivalent angles that follow from (the idea of) parallelism simultaneously constitute the angle sum to be 180°. That this is so can be discovered over and over again because (necessarily written) proof-accounts describe their own work. That is, it is precisely "in this particularistic way, the generality of our proof-account's description was evinced in and as the lived, seen, material details of the proof" (LIVINGSTON, 1987, p.108). The very nature of geometry as objectivity science arises from the demonstrability and visibility of its procedures in the living/lived (subjective) work of proving. Anyone may reproduce the living/lived work anywhere. In sum, therefore, we realize that the "generality of our proof both is in and not in the proof-account; it is in that proof-account through the pairing of that account with its lived-work" (p.108). [28]
In this brief description, we see how the living/lived work of producing, seeing, and labeling the angles is actually accomplished. This drawing, seeing, and labeling is available to those present; this drawing, seeing, and labeling makes the work objectively available to those present. But this living/lived work does not (and cannot) appear in the proof account proper, where the lines and labels appear disengaged from the actual drawing, seeing, and labeling. All of these involve our living/lived body in the manner described in Subsection 1.1 for the eyes' work that makes a cube from a set of lines. Seeing an angle involves fewer lines, but nevertheless requires the movement of the eye that puts into relation the two unfolding lines, the half planes, and the seeing of the intersecting planes against the background (generally white). The account that we might find in textbooks is disengaged from this living/lived work, but it may serve as a resource on the part of the learner, to relive the living/lived work of proving in and through his/her own living praxis of drawing, seeing, and labeling. HUSSERL (1939) accounts of the relation between accounts and the lived work in this way: In textbooks the actual production of the primal geometrical idealities is surreptitiously substituted by means of drawn figures that render concepts sensibly intuitable. It is up to the student to find in his/her own living/lived work the practical relevance, which in the present example would be the proof-specific relevance of the lines, markings, naming, and so forth. [29]
We can see that in this pairing of proof account and lived work of proving there is the possibility of a particular type of pedagogy. In fact it has been said that the proof account is "completely and hopelessly a pedagogic object—it teaches the lived-work that it itself described" (LIVINGSTON, 1987, p.104). This is so because we can see in it a formulation of the living/lived work that is described, much like an instruction that presents both what is to be done and what will be found as an outcome of the actions. However, this condition still does not solve the ultimate problem of the difference between the account and the lived work: the students have to find in their own living actions the relevance of this or that definition, this or that instruction, this or that description of an outcome. There is a surplus in the transitivity of the living/lived action over its ideation (LEVINAS, 1971) that constitutes the difference between living/lived work and any account thereof. [30]
In this section, I articulate but the beginning of an analysis that indicates the nature of the lived work as distinct from the objective accounts produced and handed down for millennia from the ancient Greek to the present day. The accounts are objectively available to all the generations; the lived (subjective) work has to be enacted each and every time by the person actually doing or following (observing) the proof. In this way, the subjective enactment of geometry and the objectively available account have to be intertwined to make geometry the objective historical science that it is. The living/lived work has nothing to do with a mental construction, as the movements underlying the (intentional) drawing of a line emerge from experiences that have nothing at all to do with intentions (ROTH, in press). These are originary movements that have nothing do with the "(embodied) image schematas" of cognitive science and embodiment/enactivist accounts but may be thought of as archetypal corporeal-kinetic forms or as kinetic melodies that would enable any such schemata, if they were to exist at all (SHEETS-JOHNSTONE, 2009). [31]
In a text on the formal structures of practical action, GARFINKEL and SACKS (1986) propose a way of theorizing the ways in which accounts of structures and the work that brings these structures about are related (Figure 8). Thus, the expression "doing [proving the sum of the internal angles of a triangle is 180°]" consists of two parts. The text between brackets "[]" topicalizes a particular practice that social scientists and educational researchers might be interested in; the text is a gloss of what a researcher or lay participant might say that is happening. For example, observing a student, a teacher might explain to the researcher visiting the classroom that the former is "proving the sum of the internal angles of a triangle is 180°." This text is the account for what is currently happening. Similarly, if asked by the researcher what she has been doing, the student might gloss, "I was proving that the sum of the internal angles of a triangle is 180°." Almost all research in the social sciences and education is of this kind; this kind of research sometimes is referred to as formal analysis. Research methods are provided in articles to articulate how the researchers arrived at identifying the structures that appear between the gloss marks (i.e., between "[" and "]"). But formal analysis does not capture the first part of the expression: it misses the "doing." This moment of the expression allows us to ask the research question, paraphrasing GARFINKEL and SACKS: "What is the work for which 'proving the sum of the internal angles of a triangle is 180°' is that work's accountable text?" or "What is the work for which 'proving the sum of the internal angles of a triangle is 180°' is that work's proper gloss?"
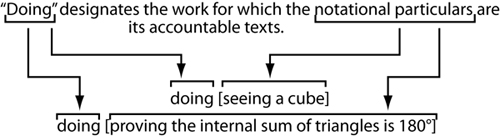
Figure 8: According to GARFINKEL and SACKS (1986), any social structure involves the practical work and that work's accountable
text. [32]
In contrast to constructive formal analysis, ethnomethodology is interested in specifying the work by means of which the structures are produced that are accounted for and glossed by the bracketed texts. In other words, the question ethnomethodology pursues is that in the living/lived work, for example, of proving that the internal sum of a triangle (on the Euclidean plane) is 180°. Once we know the organization of the living/lived work, we will be able to predict the kinds of results people produce in the same manner as we can predict what kind of entities people will see when looking at the diagram known as the Necker Cube. However, from knowing the accounts, we cannot infer the nature of the lived work. For this reason, phenomenological and ethnomethodological accounts of mathematics are related to formal analyses—whether quantitative or qualitative (e.g., phenomenography)—in asymmetrically alternate ways (GARFINKEL, 1996). This is not to say that ethnomethodology disputes the accounts provided by formal analysis; those achievements can be demonstrated and are demonstrated in and as of the outcomes of the living/lived work of doing mathematics (or science, see ROTH, 2009). This asymmetry is radical and incommensurable, but nevertheless obtains to related aspects of mathematics. Ethnomethodology (as phenomenology) is not in the business of interpreting signs that people produce. Rather, its "fundamental phenomenon and its standing technical preoccupation in its studies is to find, collect, specify, and make instructably observable the endogenous production and natural accountability of immoral familiar society's most ordinary organizational things in the world, and to provide for them both and simultaneously as objects and procedurally, as alternate methodologies" (p.6). The two examples I use here constitute such materials that allow readers, in and through engaging the work specified, to experience the living/lived, worksite-specific (inherent lived) praxis of doing mathematics. [33]
The upshot of this approach is that no account can get us closer to the actual living/lived experience of doing mathematics, even when and precisely because persons retrospectively talk about their living/lived mathematical experiences. This is so because these accounts inherently involve representations of the experience, that is, means of making some past experience present again. We do not get to these experiences themselves. In any instance imaginable, these representations—the means of making a past presence present again—are different from the living/lived work in the living present. Only metaphysics will make a claim to the contrary, because it has not recognized that ever since the Greek antiquity, scholars have attempted to access living/lived Being (Sein, Être) in and through externalities, that is, beings (Seiendes, êtant, representation). Being (capital B) and beings differ, though in metaphysical accounts of knowing and learning (which includes all forms of constructivism from Kant to the present day), the latter are freely substituted for the former (e.g., HEIDEGGER, 1982 [1943]). Therefore, the dehiscence of Being and beings is never recognized—but this is precisely the divide that I see between all forms of formal analysis and ethnomethodology, the former being concerned with beings (identifiable, identified structures) and the latter with Being, the never-ending living/lived labor of producing the structures identified in the asymmetrically alternate way in formal analyses. [34]
Readers will notice that in my approach to lived experience generally and to lived mathematical experience specifically, I am not interested in asking people how they have felt while engaging in this or that mathematical task. Any response I might receive is only a representation of the living/lived work filtered through the particular perspectives of the person. It has been noticed that what a practitioner has to say retrospectively about what s/he has done does not get us any closer to the lived praxis than what a theoretician says (BOURDIEU, 1980). Accounts of experience are as far from experience as any other description and account; they constitute but rationalizations of an originary event given everything else that we have experienced and learned since then. We know very well—as the popular adage goes—that hindsight always has 20/20 vision. Retrospective accounts always and continuously are subject to change in the face of new experiences and forms of evidence (HUSSERL, 1980 [1928]); what I get from people when I ask for accounts of experience, therefore, depends on when and under what conditions I ask.2) What I am interested in instead is this: (a) the enabling of a situation whereby the interested reader experiences the living/lived work of mathematics described (e.g., while doing the entire proof, including the drawing, seeing, concluding) and (b) an understanding of the fundamental living/lived processes that enable this or that experience (e.g., how we come to see a cube as a cube, a line as a line, etc.). [35]
The kind of distinctions I make in the preceding section allows us to move from accounts of doing mathematics to the actual living/lived labor (work). The two stand in an incommensurably and asymmetrically alternate relation. Thus, I am not interested in the interpretation of signs people produce but in the living/lived labor of doing mathematics. That is, I am not interested in local practices as texts that are interpreted for their "meaning." Rather, I am interested in accessing the living/lived labor of mathematics as events that are "in detail identical with themselves, and not representative of something else" (GARFINKEL, 1996, p.8). This requires attention to the "witnessably recurrent details of ordinary everyday practices," which literally "constitute their own reality" (p.8). We see above that knowing the work allows us to specify the structures that formal analytic procedures identify. This means, that
"you can use ethnomethodology to recover in phenomenal ordered details—in a phenomenal field of ordered details the work that makes up, at the worksite, the design, administration, and carrying off of investigations with the use of formal analytic practices. You can't do it the other way around" (p.10). [36]
Much of the living/lived work goes unnoticed—not in the least discoverable in the disattention that formal analysts pay to the living/lived work of doing mathematics. In fact, phenomenological analyses that focus on Life show that it remains invisible, especially to the so-called sciences of life, biology (HENRY, 2000). However, under special circumstances, parts of this work tends to be exhibited in situations of trouble, for example, when experienced scientists struggle with the classification of a specimen (e.g., ROTH, 2005) or when scientists struggle with providing an expert reading of a graph even though it was taken from an introductory course of their own domain (e.g., ROTH, 2008). With respect to research method, BOURDIEU (1992) suggests that what really matters in and to praxis is made available and perceivable only in the actual living/lived work of doing research—one has to experience it to be able to see it. [37]
To allow readers to (re-) live the work in and through their own living/lived bodies, reading or hearing accounts are insufficient. What research of the living/lived mathematics experience can do is
to provide for situations that make the phenomenon instructably observable such that in doing what the instructions say, the reader experiences in and through his/her living/lived labor the relevant mathematics; the phenomenological investigations of seeing a cube and proving the angle sum (work is only partially detailed) would be of that kind.
to provide something like a musical score, which, when readers actually "play the tune," allows them to live the mathematical conversations presented in the same way as musicians live the music written by some classical composer who in most cases no longer lives. We provided instructions for such an approach elsewhere (ROTH & BAUTISTA, in press). [38]
In summary, therefore, to get at the living/lived work, we need to go about research differently than what formal analysis does. There is no difference whether formal analysis denotes itself as qualitative (including phenomenography) or as quantitative. Distinctly different are phenomenological and ethnomethodological approaches, because they are concerned with the living/lived work of doing mathematics. No retrospective account can get at this because of the inherent, unavoidable dehiscence between Being (Sein, Être) and beings (Seiendes, étant), presence and the making present of the present (representation). But we have to inquire into the living/lived work, because this is the only way accessible to the "inner-historical," nature of mathematics, the very problem of its objectivity continually re/produced living/lived (subjective) sense-building and sense-producing work of everyone in the culture doing mathematics (HUSSERL, 1939). We cannot understand mathematics as a living/lived form of life unless we gain access to the very engine that keeps it alive, produces and transforms it across generations: the living/lived work of doing mathematics. [39]
In qualitative research generally and in qualitative mathematics education research specifically and in qualitative social science research generally, we must be careful about the relationship between method and the objects of our studies—lest we open ourselves to charges of "making it up as we go." HUSSERL (1980 [1928]) shows how accounts of experiences change as some original experience "sinks" into the past and the more apprehensions come to lie between the present now and the represented (remembered) now. When living/lived experiences are accounted for, the very nature of representation, its non-self-identical nature, is the origin of the different "interpretations" that may be attributed by the same individual over time or by different individuals at the same time to some event. These different accounts are not what I am interested in; I leave the articulation of such different experiences to phenomenography. What I am interested in is the structure of the real living/lived work that makes those accounts possible. It is this second way in which any phenomenon can be lived—indelibly grounded in our living/lived body (flesh, Leib, chair) that never leaves us and that constitutes the very possibility for community (HENRY, 2003)—that I am interested in accessing and making accessible. This requires, as HENRY's (2005) book title suggests, learning to "see the invisible," or, more apt, learning to experience what can only be obliquely pointed to by means of language. [40]
This article is based on a presentation at the WISDOMe conference, University of Wyoming, September 9, 2010. The research was supported by grants from the Social Sciences and Humanities Research Council of Canada concerned with the changing natures of thinking and speaking in human development.
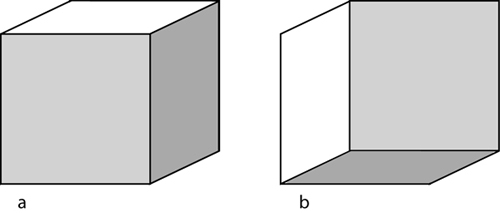
Figure A1: The two cubes that participants in psychological studies tend to report seeing in Figure 1.
1) Praxis denotes the real situation where the living/lived work occurs; it generally is not characterized by thematization and "metacognition." Practices refer to the patterned action and therefore denotes something apparent to a theoretical gaze rather than to the regard of the practitioner. <back>
2) HUSSERL (1980 [1928]) calls this the "running-off mode," whereby phenomena "sink" into the past and are seen through a continually changing horizon of the present as well as backward through all other time points that have been running off since. <back>
Bourdieu, Pierre (1980). Le sens pratique. Paris: Les Éditions de Minuit.
Bourdieu, Pierre (1992). The practice of reflexive sociology (The Paris workshop). In Pierre Bourdieu & Loic J.D. Wacquant, An invitation to reflexive sociology (pp.216-260). Chicago: University of Chicago Press.
Davis, Philip J. & Hersh, Reuben (1981). The mathematical experience. Boston, MA: Houghton Mifflin.
Garfinkel, Harold (1996). Ethnomethodology's program. Social Psychology Quarterly, 59, 5-21.
Garfinkel, Harold (2002). Ethnomethodology’s program: Working out Durkheim’s aphorism. Lanham, NY: Rowman & Littlefield.
Garfinkel, Harold & Sacks, Harvey (1986). On formal structures of practical action. In Harold Garfinkel (Ed.), Ethnomethodological studies of work (pp.160-193). London: Routledge & Kegan Paul.
Greiffenhagen, Christian (2008). Video analysis of mathematical practice? Different attempts to "open up" mathematics for sociological investigation. Forum Qualitative Sozialforschung / Forum: Qualitative Social Research, 9(3), Art. 32, http://nbn-resolving.de/urn:nbn:de:0114-fqs0803323 [Accessed: November 29, 2010].
Greiffenhagen, Christian & Sharrock, Wes (2005). Gestures in the blackboard work of mathematics instruction. Proceedings of 2nd Conference of the International Society for Gesture Studies, http://gesture-lyon2005.ens-lyon.fr/article.php3?id_article=234 [Accessed November 29, 2010]
Greiffenhagen, Christian & Sharrock, Wes (2008). School mathematics and its everyday other? Revisiting Lave's "Cognition in Practice". Educational Studies in Mathematics, 69, 1-21.
Heidegger, Martin (1977 [1950]). Holzwege. Frankfurt/M.: Vittorio Klostermann.
Heidegger, Martin (1982). Parmenides. Frankfurt/M.: Vittorio Klostermann. [Lectures held 1942/1943]
Heidegger, Martin (2000 [1954]). Vorträge und Aufsätze. Frankfurt/M.: Vittorio Klostermann.
Henry, Michel (1990). Phénoménologie matérielle. Paris: Presses Universitaires de France.
Henry, Michel (2000). Incarnation: Une philosophie de la chair. Paris: Seuil.
Henry, Michel (2003). Phénoménologie de la vie tome 1: De la phénoménologie. Paris: Presses Universitaires de France.
Henry, Michel (2005). Voir l'invisible: sur Kandinsky. Paris: Presses Universitaires de France.
Husserl, Edmund (1939). Die Frage nach dem Ursprung der Geometrie als intentional-historisches Problem. Revue internationale de philosophie, 1, 203-225.
Husserl, Edmund (1980 [1928]). Vorlesungen zur Phänomenologie des inneren Zeitbewußtseins. Tübingen: Max Niemeyer.
Levinas, Emmanuel (1971). Totalité et infini: Essai sur l'extériorité. La Haye: Martinus Nijhoff.
Livingston, Eric (1986). The ethnomethodological foundations of mathematics. London: Routledge and Kegan Paul.
Livingston, Eric (1987). Making sense of ethnomethodology. London: Routledge & Kegan Paul.
Luria, Aleksandr R. (1973). The working brain. Harmondsworth: Penguin Books.
Marion, Jean-Luc (2002). Being given: Toward a phenomenology of givenness. Stanford, CA: Stanford University Press.
Nancy, Jean-Luc (2003). Le fond de l'image. Paris: Galilée.
Roth, Wolff-Michael (2005). Making classifications (at) work: Ordering practices in science. Social Studies of Science, 35, 581-621.
Roth, Wolff-Michael (2008). The dawning of signs in graph interpretation. Luis Radford, Gert Schubring & Falk Seeger (Eds.), Semiotics in mathematics education (pp.83-102). Rotterdam: Sense.
Roth, Wolff-Michael (2009). Specifying the ethnomethodological "what more?" Cultural Studies of Science Education, 4, 1-12.
Roth, Wolff-Michael (2010). Incarnation: Radicalizing the embodiment of mathematics. For the Learning of Mathematics, 30(2), 2-9.
Roth, Wolff-Michael (in press). Geometry as objective science in elementary classrooms: Mathematics in the flesh. New York: Routledge.
Roth, Wolff-Michael & Bautista, Alfredo (in press). Transcriptions, mathematical cognition, and epistemology. The Montana Mathematics Enthusiast, 8(2).
Sartre, Jean-Paul (1956). Being and nothingness. New York: Gramercy Books.
Sheets-Johnstone, Maxine (2009). The corporeal turn: An interdisciplinary reader. Exeter, UK: Imprint Academic.
von Uexküll, Jacob (1973). Theoretische Biologie. Frankfurt/M.: Suhrkamp.
Wolff-Michael ROTH is Lansdowne Professor of Applied Cognitive Science at the University of Victoria. He conducts transdisciplinary research on knowing and learning across the life span, mostly focusing on mathematical and scientific content. His recent publications include Talk about Careers in Science (2010, Rotterdam: Sense Publishers; edited with Pei-Ling HSU), Language, Learning, Context (2010, London: Routledge), Analyzing Communication: Praxis of Method (2010, Rotterdam: Sense Publishers; with Pei-Ling HSU), Dialogism: A Bakhtinian Perspective on Science and Learning (2009, Rotterdam: Sense Publishers), and Mathematical Representation at the Interface of Body and Culture (2009, Charlotte, NC: Information Age Publishing, edited).
Contact:
Wolff-Michael Roth
Lansdowne Professor
MacLaurin Building A548
University of Victoria
Victoria, BC, V8W 3N4
Canada
E-mail: mroth@uvic.ca
URL: http://www.educ.uvic.ca/faculty/mroth/
Roth, Wolff-Michael (2011). Researching Living/Lived Mathematical Work [40 paragraphs]. Forum Qualitative Sozialforschung / Forum: Qualitative Social Research, 12(1), Art. 31, http://nbn-resolving.de/urn:nbn:de:0114-fqs1101318.